题型:填空题 题类:其他 难易度:中档
年份:2018
学生的体质与学生饮食的科学性密切相关,营养学家指出,高中学生良好的日常饮食应该至少提供\(0.075 kg\)的碳水化合物,\(0.06 kg\)的蛋白质,\(0.06 kg\)的脂肪\(.\)已知\(1 kg\)食物\(A\)含有\(0.105 kg\)碳水化合物,\(0.07 kg\)蛋白质,\(0.14 kg\)脂肪,花费\(28\)元;\(1 kg\)食物\(B\)含有\(0.105 kg\)碳水化合物,\(0.14 kg\)蛋白质,\(0.07 kg\)脂肪,花费\(21\)元\(.\)为了满足高中学生日常饮食的营养要求,每天合理搭配食物\(A\)和食物\(B\),则最低花费是________元.
题型:填空题 题类:其他 难易度:中档
年份:2018
\((1)\)某科技公司在江苏、浙江、上海、安徽四省份分别设有\(200\)、\(180\)、\(70\)、\(150\)个销售点,为调查产品的销售与售后服务等情况,需要利用分层抽样的方法从这些销售点中抽取一个容量为\(100\)的样本,则需要从安徽省抽取________个销售点.
\((2)\)已知实数\(x\),\(y\)满足\(\begin{cases} & y\leqslant 4-2x \\ & x-2y\leqslant 2 \\ & x\geqslant 1 \end{cases}\),则\(\dfrac{y-1}{x+2}\)的取值范围为________.
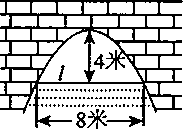
\((3)\)如图是抛物线形拱桥,当水面在\(l\)时,拱顶离水面\(4\)米,水面宽\(8\)米\(.\)水面下降\(1\)米后,水面宽________米.
\((4)\)设曲线\(y=x^{n+1}(n∈N^{*})\)在点\((1,1)\)处的切线与\(x\)轴的交点的横坐标为\(x_{n}\),则\({{\log }_{2018}}^{{{x}_{1}}}+{{\log }_{2018}}^{{{x}_{2}}}+{{\log }_{2018}}^{{{x}_{3}}}+\cdots +{{\log }_{2018}}^{{{x}_{2017}}}\)的值为________.
题型:填空题 题类:其他 难易度:难
年份:2018
\((1)\) 某企业生产甲、乙两种产品均需用\(A\),\(B\)两种原料,已知生产\(1\)吨每种产品所需原料及每天原料的可用限额如表所示,如果生产\(1\)吨甲、乙产品可获得利润分别为\(4\)万元、\(3\)万元,则该企业每天可获得最大利润为______ 万元
| 甲 | 乙 | 原料限额 |
\(A(\)吨\()\) | \(2\) | \(5\) | \(10\) |
\(B(\)吨\()\) | \(6\) | \(3\) | \(18\) |
\((2)\) 已知\(x{ > }1\),则函数\(y{=}\dfrac{x^{2}{+}x{+}1}{x{-}1}\)的最小值为______.
\((4)\) 设等差数列\(\{ a_{n}\}\)的前\(n\)项和为\(S_{n}\),若\(a_{4}{⩾}8\),\(a_{5}{⩽}10\),则\(S_{6}\)的最小值为______________.