题型：填空题 题类：期末考试 难易度：较难
年份：2018
\((1)\)执行如图所示的程序框图，\(S\)为输出的结果，则二项式\({{(S\sqrt{x}-\dfrac{3}{\sqrt{x}})}^{6}}\)的展开式中的常数项是________．
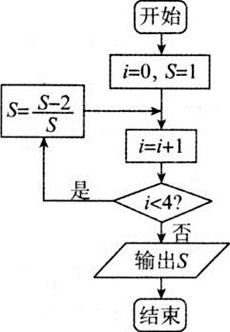
\((2)\)已知\(f(x)\)是定义在\(R\)上的奇函数，当\(x > 0\)时，，\(f(x)=x^{2}-2x\)，则不等式，\(f(x) > x\)的解集用区间表示为________．
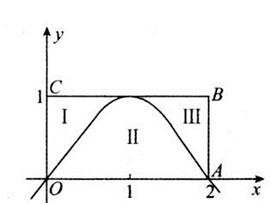
\((3)\)如图，一矩形靶\(OABC\)由抛物线\(y=-x^{2}+2x\)分成\(I\)区、Ⅱ区、Ⅲ区三个区域，现随机向该靶射击一次\((\)假定每次射击都不会脱靶\()\)，则击中Ⅲ区的概率为________．
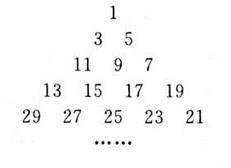
\((4)\)已知从\(1\)开始的连续奇数蛇形排列形成宝塔形数表，第一行为\(1\)，第二行为\(3\)，\(5\)，第三行为\(7\)，\(9\)，\(11\)，第四行为\(13\)，\(15\)，\(l7\)，\(19\)，\(……\)，如图所示，在宝塔形数表中位于第\(i\)行、第\(j\)列的数记为\(a_{i,j}\)，比如\(a_{3,2}=9\)，\(a_{4,2}=15\)，\(a_{5,4}=23\)，若\(a_{i,j}=2017\)，则\(i+j=\)________．
题型：填空题 题类：期末考试 难易度：较难
年份：2018
给出下列四个命题中：
\(①\)命题：\(\exists x\in R,\sin x+\cos x=\sqrt{3}\)；\(②\exists x\in \left( -\infty ,0 \right),{{2}^{x}} < {{3}^{x}}\)
\(③\forall x\in R,{{e}^{x}}\geqslant x+1\)\(④\)对\(\forall \left( x,y \right)\in \left\{ \left( x,y \right)\left| 4x+3y-10=0 \right. \right\}\)，则\({{x}^{2}}+{{y}^{2}}\geqslant 4\)．
其中所有真命题的序号是___________．
题型：填空题 题类：期末考试 难易度：较难
年份：2018
\((1)\)计算：\({{(\dfrac{2}{3})}^{0}}+3\times {{(\dfrac{9}{4})}^{-\frac{1}{2}}}+(\lg 4+\lg 25)\)的值是______．
\((2)\)若\(x\)，\(y\)满足约束条件\(\begin{cases} & x+y-5\leqslant 0 \\ & 2x-y-1\geqslant 0 \\ & x-2y+1\leqslant 0 \end{cases}\)，则\(z=2x+y\)的最小值为______
\((3)\)已知向量\(\overrightarrow{a}=(-1,2)\)，\(\overrightarrow{b}=(m,1)\)，若向量\(\overrightarrow{a}+\overrightarrow{b}\)与\(\overrightarrow{a}\)垂直，则\(m=\)______．
\((4)\)九章算术是我国古代数学成就的杰出代表其中方田章给出计算弧田面积所用的经验公式为：弧田面积\(=\dfrac{1}{2} (\)弦\(×\)矢\(+\)矢\({\,\!}^{2})·\)弧田，由圆弧和其所对弦所围成公式中“弦”指圆弧对弦长，“矢”等于半径长与圆心到弦的距离之差，按照上述经验公式计算所得弧田面积与实际面积之间存在误差现有圆心角为\(\dfrac{2}{3}\pi \)，弦长等于\(9\)米的弧田，按照\(《\)九章算术\(》\)中弧田面积的经验公式计算所得弧田面积与实际面积的差为______．
题型：填空题 题类：期末考试 难易度：较难
年份：2018
\(13.(1)\)如果\(\cos \alpha =\dfrac{1}{3}\)，且\(\alpha \)是第四象限的角，那么\(\cos \left(α+ \dfrac{π}{2}\right)= \)_____________。
\((2)\)设变量\(x,y\)满足约束条件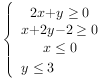
，则目标函数\(z=x+y\)的最大值为_______________。
\((3)\)若实数\(x\)，\(y\)满足\(xy > 0\)，则\(\dfrac{x}{x+y}+\dfrac{2y}{x+2y}\)的最大值为______________。
\((4)\)非零向量\(\overrightarrow{m},\overrightarrow{n}\)的夹角为\(\dfrac{\pi }{3}\)，且满足\(\left| \overrightarrow{n} \right|=\lambda \left| \overrightarrow{m} \right|\left( \lambda > 0 \right)\)，向量组\(\overrightarrow{{{x}_{1}}},\overrightarrow{{{x}_{2}}},\overrightarrow{{{x}_{3}}}\)由一个\(\overrightarrow{m}\)和两个\(\overrightarrow{n}\)排列而成，向量组\(\overrightarrow{{{y}_{1}}},\overrightarrow{{{y}_{2}}},\overrightarrow{{{y}_{3}}}\)由两个\(\overrightarrow{m}\)和一个\(\overrightarrow{n}\)排列而成，若\(\overrightarrow{{{x}_{1}}}\cdot \overrightarrow{{{y}_{1}}}+\overrightarrow{{{x}_{2}}}\cdot \overrightarrow{{{y}_{2}}}+\overrightarrow{{{x}_{3}}}\cdot \overrightarrow{{{y}_{3}}}\)所有可能值中的最小值为\(4{{\overrightarrow{m}}^{2}}\)，则\(\lambda =\)_________．
