代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：1788选择本页全部试题

题型：解答题题类：模拟题难易度：中档
新
年份：2020

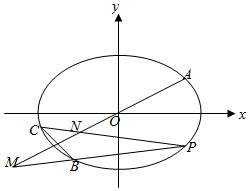如图，已知椭圆\(Γ\)：\( \dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} =1(a > b > 0)\)经过不同的三点\(A( \dfrac { \sqrt {5}}{2} , \dfrac { \sqrt {5}}{4} )\)，\(B(- \dfrac {1}{2} , - \dfrac {3}{4} )\)，\(C(C\)在第三象限\()\)，线段\(BC\)的中点在直线\(OA\)上．
\((\)Ⅰ\()\)求椭圆\(Γ\)的方程及点\(C\)的坐标；
\((\)Ⅱ\()\)设点\(P\)是椭圆\(Γ\)上的动点\((\)异于点\(A\)、\(B\)、\(C)\)且直线\(PB\)、
\(PC\)分别交直线\(OA\)于\(M\)、\(N\)两点，问\(|OM|\boldsymbol{⋅}|ON|\)是否为定值？
若是，求出定值；若不是，请说明理由．

查看解析收藏纠错

+选题
题型：选择题题类：模拟题难易度：中档
新测
年份：2020

设数列\(\{a _{n} \}\)满足\(a _{n+2} -2a _{n+1} +a _{n} > 1\)对任意的\(n∈N*\)恒成立，则下列说法正确的是\((\:\:\:\:)\)

A.\(a _{n+2} a _{n} > a _{n+1} ^{2}\) B.数列\(\{a _{n} \}\)单调递增 C.存在正整数\(M\)，当\(n > M\)时，\(a _{n+1} > a _{n} +n\)恒成立 D.存在正整数\(M\)，当\(n > M\)时，\(a_{n} > \dfrac {n^{2}}{3}\)恒成立

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

\(\triangle ABC\)中，\(∠ABC=90°\)，\(AB=2\)，\(BC=1\)，点\(D\)在线段\(AB\)上，\(∠ACD=45°\)，则\(BD=\)______，\(\triangle ACD\)面积是______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：中档
新
年份：2020

已知函数\(f(x)=2\sin x\cos (x- \dfrac {π}{6} ).\)
\((\)Ⅰ\()\)求\(f(x)\)的最小正周期和对称轴方程：
\((\)Ⅱ\()\)若\(f(x)\)在\(x∈[ \dfrac {π}{4}-a, \dfrac {π}{4}+a](a > 0)\)上是增函数，求实数\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：中档
新
年份：2020

在四棱锥\(P-ABCD\)中，四边形\(ABCD\)为直角梯形，\(AD/\!/BC\)，\(AB⊥AD\)，\(AD=2BC\)，\(AB=1\)，\(\triangle APD\)为等腰直角三角形，且\(PA=DP=2\)，\(E\)为\(PA\)中点．
\((\)Ⅰ\()\)求证：\(EB/\!/\)平面\(PCD\)；
\((\)Ⅱ\()\)若二面角\(P-AD-B\)的大小为\( \dfrac {3π}{4}\)，求直线\(CD\)与平面\(PAB\)所成角的正弦值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：中档
新
年份：2020

已知数列\(\{a _{n} \}\)和\(\{b _{n} \}\)满足：\(b _{3} -b _{2} =3a _{1} =6\)，\(a_{1}a_{2}a_{3}…a_{n}=( \sqrt {2})^{b_{n}}(n∈N^{*})\)且数列\(\{ \dfrac {b_{n}}{n}\}\)为等差数列．设\(c _{n} = \dfrac {(-1)^{n}}{a_{n}}+ \dfrac {1}{b_{n}}\)，数列\(\{c _{n} \}\)的前\(n\)项和为\(S _{n}\)．
\((\)Ⅰ\()\)求\(\{a _{n} \}\)与\(\{b _{n} \}\)的通项公式：
\((\)Ⅱ\()\)若对于任意\(n∈N*\)均有\(S _{k} \leqslant S _{n}\)，求正整数\(k\)的值．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

已知数列\(\{{a}_{n}\}\)为等差数列，若\(\dfrac{{{a}_{11}}}{{{a}_{10}}} < -1\)，且它的前\(n\)项和\({S}_{n}\)有最大值，则使得\({S}_{n} > 0\)的\(n\)的最大值为___________．

查看解析收藏纠错

+选题
题型：填空题题类：模拟题难易度：中档
新
年份：2020

设椭圆\( \dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} =1(a > b > 0))\)的左焦点为\(F\)，过椭圆上一点\(A\)作椭圆的切线交\(y\)轴于点\(Q\)若\(∠QFO= \dfrac {π}{4}\)，\(∠QFA= \dfrac {π}{6}\)，则此椭圆的离心率为______．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：中档
新
年份：2020

已知抛物线\(C\)：\(x ^{2} =2py(p > 0)\)的焦点为\(F\)，过\(F\)且斜率为\(1\)的直线与\(C\)交于\(A\)，\(B\)两点，\(|AB|=8\)．
\((1)\)求\(C\)的方程；
\((2)\)过点\(D(1 , 2)\)的直线\(l\)交\(C\)于点\(M\)，\(N\)，点\(Q\)为\(MN\)的中点，\(QR⊥x\)轴交\(C\)于点\(R\)，且\( \overrightarrow {QR}= \overrightarrow {RT}\)，证明：动点\(T\)在定直线上．

查看解析收藏纠错

+选题
题型：选择题题类：模拟题难易度：中档
新测
年份：2020

已知\(F _{1}\)，\(F _{2}\)分别为双曲线\(C\)：\( \dfrac {x^{2}}{a^{2}}- \dfrac {y^{2}}{b^{2}} =1\)的左、右焦点，过点\(F _{2}\)的直线与双曲线\(C\)的右支交于\(A\)，\(B\)两点，设点\(H(x _{H} , y _{H} )\)，\(G(x _{G} , y _{G} )\)分别为\(\triangle AF _{1} F _{2}\)，\(\triangle BF _{1} F _{2}\)的内心，若\(|y _{H} |=3|y _{G} |\)，则双曲线离心率的取值范围为\((\:\:\:\:)\)

A.\([2 , +∞)\) B.\((1 , \sqrt {2} ]\) C.\((1 , 2]\) D.\((1 , 2)\)

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心