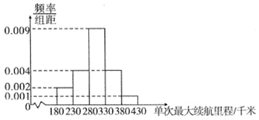
某汽车公司最近研发了一款新能源汽车，并在出厂前对100辆汽车进行了单次最大续航里程的测试．现对测试数据进行分析，得到如图所示的频率分布直方图：
（1）估计这100辆汽车的单次最大续航里程的平均值同一组中的数据用该组区间的中点值代表）．
（2）根据大量的汽车测试数据，可以认为这款汽车的单次最大续航里程X近似地服从正态分布N（μ，σ
2），经计算第（1）问中样本标准差s的近似值为50．用样本平均数x作为μ的近似值，用样本标准差s作为a的估计值，现任取一辆汽车，求它的单次最大续航里程恰在250千米到400千米之间的概率．
参考数据：若随机变量ξ服从正态分布N（μ，σ
2），则P（μ-σ＜ξ≤μ+σ）≈0.6827，P（μ-3σ＜ξ≤μ+3σ）≈0.9973，P（μ-2σ＜ξ≤μ+2σ）≈0.9545．
（3）某汽车销售公司为推广此款新能源汽车，现面向意向客户推出“玩游戏，送大奖”活动，客户可根据拋掷硬币的结果，操控微型遥控车在方格图上行进，若遥控车最终停在“胜利大本营”，则可获得购车优惠券3万元．已知硬币出现正、反面的概率都是0.5，方格图上标有第0格、第1格、第2格、……、第20格．遥控车开始在第0格，客户每掷一次硬币，遥控车向前移动一次．若掷出正面，遥控车向前移动一格（从k到k+1），若掷出反面，遥控车向前移动两格（从k到k+2），直到遥控车移到第19格（胜利大本营）或第20格（失败大本营）时，游戏结束．设遥控车移到第n（l＜n＜19）格的概率为，试证明{P
n-P
n-1}是等比数列，并求参与游戏一次的顾客获得优惠券金额的期望值．
（c-acosB）=bsinA． 
，求b+c的最大值． 
的直线l被圆C截得的弦AB的长为4，求直线l的倾斜角；
，求tanC． 
·
＝2，cos B＝
，b＝3.求：
上的点到椭圆一个焦点的距离的最大值是最小值的3倍，且点
在椭圆E上．