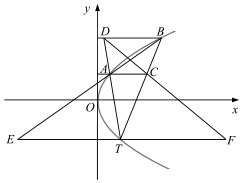
如图，在平面直角坐标系\(xOy\)中，已知点\(T(1,t)(t < 0)\)到抛物线\(y^{2}=2px(p > 0)\)焦点的距离为\(2\)．
\((1)\)求\(p\)，\(t\)的值；
\((2)\)设\(A\)，\(B\)是抛物线上异于\(T\)的两个不同点，过\(A\)作\(y\)轴的垂线，与直线\(TB\)交于点\(C\)，过\(B\)作\(y\)轴的垂线，与直线\(TA\)交于点\(D\)，过\(T\)作\(y\)轴的垂线，与直线\(AB\)，\(CD\)分别交于点\(E\)，\(F\)．
求证：\(①\)直线\(CD\)的斜率为定值；
\(②T\)是线段\(EF\)的中点．