已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}}+ \dfrac {y^{2}}{b^{2}}=1(a > b > 0)\)过点\((1, \dfrac {3}{2})\)且离心率为\( \dfrac {1}{2}\)．
\((1)\)求椭圆\(C\)的标准方程；
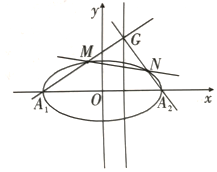
\((2)\)若\(A _{1}\)，\(A _{2}\)分别为\(C\)的左、右顶点，\(G\)为直线\(x=1\)上的任意一点，直线\(GA _{1}\)，\(GA _{2}\)分别与\(C\)相交于\(M\)、\(N\)两点，连接\(MN\)，试证明直线\(MN\)过定点，并求出该定点的坐标．