已知如图\(1\)，在\({\rm Rt}\triangle ABC\)中，\(∠ACB=30°\)，\(∠ABC=90°\)，\(D\)为\(AC\)中点，\(AE⊥BD\)于\(E\)，延长\(AE\)交\(BC\)于\(F\)，将\(\triangle ABD\)沿\(BD\)折起，使平面\(ABD⊥\)平面\(BCD\)，如图\(2\)所示．

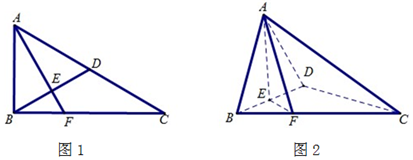
\((\)Ⅰ\()\)求证：\(AE⊥\)平面\(BCD\)；
\((\)Ⅱ\()\)求二面角\(A-DC-B\)的余弦值；
\((\)Ⅲ\()\)求三棱锥\(B-AEF\)与四棱锥\(A-FEDC\)的体积的比\((\)只需写出结果，不要求过程\()\)．