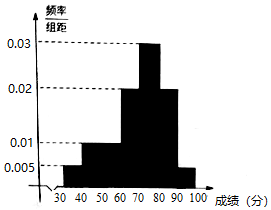
为推进中小学体育评价体系改革，某调研员从一中学\(4000\)名学生中按照男女学生比例采用分层抽样的方法，从中随机抽取了\(400\)名学生进行某项体育测试\((\)满分\(100\)分\()\)，记录他们的成绩，将记录的数据分成\(7\)组：\((30 , 40]\)，\((40 , 50]\)，\((50 , 60]\)，\((60 , 70]\)，\((70 , 80]\)，\((80 , 90]\)，\((90 , 100]\)，并整理得到如图频率分布直方图．
\((\)Ⅰ\()\)根据该频率分布直方图，估计样本数据的中位数及\(4000\)名学生的平均成绩\((\)同一组中的数据用该组区间的中点值作代表\()(\)精确到\(0.01)\)；
\((\)Ⅱ\()\)已知样本中有三分之二的男生分数高于\(60\)分，且分数高于\(60\)分的男女人数相等，试估计该校男生和女生人数的比例；
\((\)Ⅲ\()\)若测试成绩\(x < \overset{ -}{x} -2s(\)其中\( \overset{ -}{x}\)是成绩的平均值，\(s\)是标准差\()\)，则认为该生测试成绩不达标，试估计该中学测试成绩不达标人数．
参考公式：\(s^{2}= \sum\limits_{i=1}^{n}(x_{i}- \overset{ -}{x} ) ^{2} p _{i} (p _{i}\)是第\(i\)组的频率\()\)，其中\( \sqrt {2}≈1.4, \sqrt {117}≈10.8\)．