某中学调查防疫期间学生居家每天锻炼时间情况,从高一、高二年级学生中分别随机抽取100人,由调查结果得到如图的频率分布直方图:
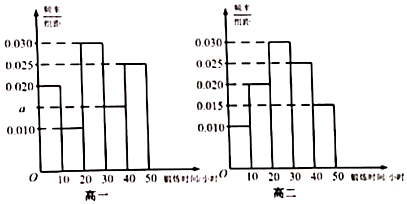
(Ⅰ)写出频率分布直方图(高一)中a的值;记高一、高二学生100人锻炼时间的样本的方差分别为s
12,s
22,试比较s
12,s
22的大小(只要求写出结论);
(Ⅱ)估计在高一、高二学生中各随机抽取1人,恰有一人的锻炼时间大于20分钟的概率;
(Ⅲ)由频率分布直方图可以认为,高二学生锻炼时间Z服从正态分布N(μ,σ
2),其中μ近似为样本平均数
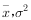
近似为样本方差,且每名学生锻炼时间相互独立,设X表示从高二学生中随机抽取10人,其锻炼时间位于(14.55,38.45)的人数,求X的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得s
2=
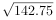
≈11.95;
②若Z~N(μ,σ
2),则P(μ-σ<z<μ+σ)=0.6826,P(μ-2σ<z<μ+2σ)=0.9544.

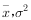 近似为样本方差,且每名学生锻炼时间相互独立,设X表示从高二学生中随机抽取10人,其锻炼时间位于(14.55,38.45)的人数,求X的数学期望.
近似为样本方差,且每名学生锻炼时间相互独立,设X表示从高二学生中随机抽取10人,其锻炼时间位于(14.55,38.45)的人数,求X的数学期望.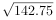 ≈11.95;
≈11.95;