如图,抛物线\(E\):\({x}^{2}=2py(p > 0) \)的焦点为\((0, \dfrac{1}{4}) \),圆心\(M\)在射线\(y=2x(x\geqslant 0) \)上且半径为\(1\)的圆\(M\)与\(y\)轴相切.
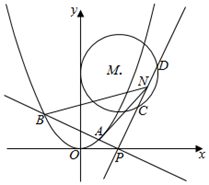
\((1)\)求抛物线\(E\)及圆\(M\)的方程;
\((2)\)过\(P(1,0) \)作两条相互垂直的直线,与抛物线\(E\)相交于\(A\),\(B\)两点,与圆\(M\)相交于\(C\),\(D\)两点,\(N\)为线段\(CD\)的中点,当\({{S}_{\vartriangle NAB}}=\dfrac{3}{2}\),求\(AB\)所在的直线方程。
