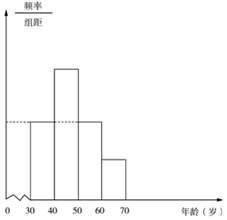某汽车公司的\(A\)型号汽车近期销量锐减，该公司为了解销量锐减的原因，就是否支持购买\(A\)型号汽车进行了市场调查，在所调查的\(1000\)个对象中，年龄在\([20,30)\)的群体有\(200\)人，支持率为\(0％\)，年龄在\([30,40)\)和\([40,50)\)的群体中，支持率均为\(3％\)；年龄在\([50,60)\)和\([60,70)\)的群体中，支持率分别为\(6％\)和\(13％\)，若在调查的对象中，除\([20,30)\)的群体外，其余各年龄层的人数分布情况如频率分布直方图所示，其中最后三组的频数构成公差为\(100\)的等差数列．
\((1)\)求年龄在\([50,60)\)群体的人数；
\((2)\)请完成\(2×2\)列联表，并根据表中的数据，判断能否在犯错误的概率不超过\(0.001\)的前提下认为年龄与支持率有关？

年龄分布 是否支持	\([30,40)\)和\([40,50)\)	\([50,60)\)和\([60,70)\)	合计
支持
不支持
合计

附表：

\(P(K^{2}\geqslant k)\)	\(0.15\)	\(0.10\)	\(0.05\)	\(0.025\)	\(0.010\)	\(0.005\)	\(0.001\)
\(k\)	\(2.072\)	\(2.076\)	\(3.841\)	\(5.024\)	\(6.635\)	\(7.879\)	\(10.828\)

\((\)参考公式：\(K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}\)，其中\(n=a+b+c+d.\)
参考数据：\(125×33=15×275\)，\(125×97=25×485)\)