如图\(1\)，\(ABCD\)是一个直角梯形，\(∠ABC=∠BAD=90\)，\(E\)为\(BC\)边上一点，\(AE\)、\(BD\)相交于\(O\)，\(AD=EC=3\)，\(BE=1\)，\(AB= \sqrt {3}.\)将\(\triangle ABE\)沿\(AE\)折起，使平面\(ABE⊥\)平面\(ADE\)，连接\(BC\)、\(BD\)，得到如图\(2\)所示的四棱锥\(B-AECD\)．

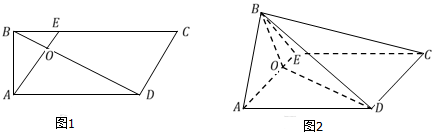
\((\)Ⅰ\()\)求证：\(CD⊥\)平面\(BOD\)；
\((\)Ⅱ\()\)求直线\(AB\)与面\(BCD\)所成角的余弦值．