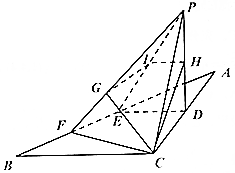如图，\(\triangle ABC\)中，\(AC=2\)，\(BC=4\)，\(∠ACB=90^{\circ}\)，\(D\)、\(E\)分别是\(AC\)、\(AB\)的中点，将\(\triangle ADE\)沿\(DE\)折起成\(\triangle PDE\)，使面\(PDE⊥\)面\(BCDE\)，\(H\)、\(F\)分别是边\(PD\)和\(BE\)的中点，平面\(BCH\)与\(PE\)、\(PF\)分别交于点\(I\)、\(G\)．
\((\)Ⅰ\()\)求证：\(IH/\!/BC\)；
\((\)Ⅱ\()\)求二面角\(P-GI-C\)的余弦值．