在四棱锥\(S-ABCD\)中，底面\(ABCD\)为长方形，\(SB⊥\)底面\(ABCD\)，其中\(BS=2\)，\(BA=2\)，\(BC=t\)，\(t\)的可能取值为：①\(t=\dfrac{1}{3}\)；②\(t=\dfrac{\sqrt{2}}{2}\)；③\(t=\dfrac{\sqrt{3}}{2}\)；④\(t=\dfrac{5}{2}\)；⑤\(t=3.\)

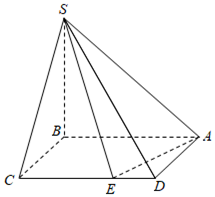
\((1)\)求直线\(AS\)与平面\(ABCD\)所成角的正弦值；
\((2)\)若线段\(CD\)上能找到点\(E\)，满足\(AE⊥SE\)，则\(t\)可能的取值有几种情况？请说理由；
\((3)\)在\((2)\)的条件下，当\(t\)为所有可能情况的最大值时，线段\(CD\)上满足\(AE⊥SE\)的点有两个，分别记为\(E_{1}\)，\(E_{2}\)，求二面角\(E_{1}-SB-E_{2}\)的大小.