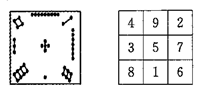
我国古代的《洛书》中记载着世界上最古老的一个幻方：如图，将\(1\)，\(2\)，…，\(9\)填入\(3×3\)的方格内，使三行，三列和两条对角线上的三个数字之和都等于\(15.\)一般地，将连续的正整数\(1,2,3,⋯,{n}^{2}\)填入\(n×n\)个方格中，使得每行，每列和两条对角线上的数字之和都相等，这个正方形叫做\(n\)阶幻方\(.\)记\(n\)阶幻方的对角线上的数字之和为\({N}_{n}\)，如图三阶幻方的\({N}_{3}=15\)，那么\({N}_{9}\)的值为\((\quad)\)