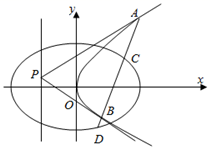
已知点\(P\)是抛物线\(C _{1}\)：\(y ^{2} =4x\)的准线上任意一点，过点\(P\)作抛物线\(C _{1}\)的两条切线\(PA\)，\(PB\)，其中\(A\)，\(B\)为切点．
\((1)\)证明：直线\(AB\)过定点，并求出定点的坐标；
\((2)\)若直线\(AB\)交椭圆\(C _{2}\)：\( \dfrac {x^{2}}{4}+ \dfrac {y^{2}}{3} =1\)于\(C\)，\(D\)两点，\(S _{1}\)，\(S _{2}\)分别是\(\triangle PAB\)，\(\triangle PCD\)的面积，求\( \dfrac {S_{1}}{S_{2}}\)的最小值．