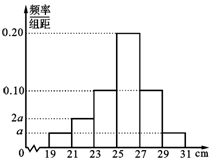为了解某品种一批树苗生长情况，在该批树苗中随机抽取了容量为\(120\)的样本，测量树苗高度\((\)单位：\(cm)\)，经统计，其高度均在区间\([19,31]\)内，将其按\([19,21),[21,23),[23,25),[25,27),[27,29),[29,31]\)分成\(6\)组，制成如图所示的频率分布直方图．其中高度为\(27cm\)及以上的树苗为优质树苗．
\((1)\)求图中\(a\)的值；
\((2)\)已知所抽取的这\(120\)棵树苗来自于\(A\)，\(B\)两个试验区，部分数据如下列联表：

	\(A\)试验区	\(B\)试验区	合计
优质树苗		\(20\)
非优质树苗	\(60\)
合计

将列联表补充完整，并判断是否有\(99.9％\)的把握认为优质树苗与\(A\)，\(B\)两个试验区有关系，并说明理由；
\((3)\)用样本估计总体，若从这批树苗中随机抽取\(4\)棵，其中优质树苗的棵数为\(X\)，求\(X\)的分布列和数学期望\(EX.\)
下面的临界值表仅供参考：

\(P(K^{2}\geqslant k_{0})\)	\(0.15\)	\(0.10\)	\(0.05\)	\(0.025\)	\(0.010\)	\(0.005\)	\(0.001\)
\(k_{0}\)	\(2.072\)	\(2.706\)	\(3.841\)	\(5.024\)	\(6.635\)	\(7.879\)	\(10.828\)

\((\)参考公式：\(K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}\)，其中\(n=a+b+c+d.)\)