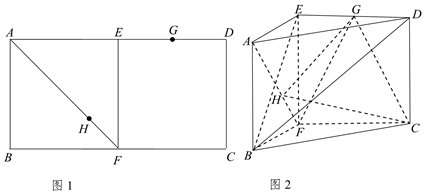
如图\(1\)，在长方形\(ABCD\)中，\(AB= \dfrac {1}{2}BC= \sqrt {2}\)，\(E\)，\(F\)分别为\(AD\)、\(BC\)的中点，\(G\)为\(ED\)的中点，点\(H\)在线段\(AF\)上，且满足\(AH=λAF.\)将正方形\(ABFE\)沿\(EF\)折起，使得直线\(EF\)与平面\(ABCD\)间的距离为\(1\)，得到如图\(2\)所示的三棱柱\(AED-BFC\)．
\((1)\)求证：\(AF⊥\)平面\(BED\)：
\((2)\)若三棱锥\(G-HFC\)的体积为\( \dfrac { \sqrt {2}}{6}\)，求\(λ\)的值．