已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} =1(a > b > 0)\)的左、右焦点和短轴的两个端点构成边长为\(2\)的正方形．
\((\)Ⅰ\()\)求椭圆 \(C\)的方程；
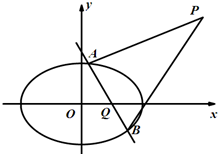
\((\)Ⅱ\()\)过点\(Q(1 , 0)\)的直线 \(l\)与椭圆\(C\)相交于\(A\)，\(B\)两点．点\(P(4 , 3)\)，记直线\(PA\)，\(PB\)的斜率分别为\(k _{1}\)，\(k _{2}\)，当\(k _{1} \boldsymbol{⋅}k _{2}\) 最大时，求直线\(l\)的方程．