法国数学家亨利•庞加莱(Jules Henri Poincare)是个每天都会吃面包的人,他经常光顾同一家面包店,面包师声称卖给庞加莱的面包平均重量是1000g,上下浮动50g.在庞加莱眼中,这用数学语言来表达就是:面包的重量服从期望为1000g,标准差为50g的正态分布.
(1)假如面包师没有撒谎,现庞加莱从该面包店任意买2个面包,求其质量均不少于1000g的概率;
(2)出于兴趣或一个偶然的念头,庞加莱每天将买来的面包称重并记录得到25个面包质量(X)的数据(单位:g)如表:
| 983 | 972 | 966 | 992 | 1010 | 1008 | 954 | 952 | 969 |
| 968 | 998 | 1001 | 1006 | 957 | 950 | 969 | 971 | 975 |
| 952 | 959 | 987 | 1011 | 1000 | 997 | 961 | | |
设从这25个面包中任取2个,其质量不少于1000g的面包数记为η,求η的分布列及E(η);
(3)庞加莱计算出这25个面包质量(X)的平均值
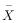
=978.72g,标准差是20.16g,认定面包师在制作过程中偷工减料,并果断举报给质检部门,质检员对面包师做了处罚,面包师也承认自己的错误,并同意做出改正.
庞加莱在接下来的一段时间里每天都去这家面包店买面包,他又认真记录了25个面包的质量,并算得它们的平均值为1002.6g,标准差是5.08g,于是庞加莱又一次将面包师举报了.
请你根据两次平均值和标准差的计算结果及其统计学意义,说说庞加莱又一次举报的理由.
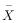 =978.72g,标准差是20.16g,认定面包师在制作过程中偷工减料,并果断举报给质检部门,质检员对面包师做了处罚,面包师也承认自己的错误,并同意做出改正.
=978.72g,标准差是20.16g,认定面包师在制作过程中偷工减料,并果断举报给质检部门,质检员对面包师做了处罚,面包师也承认自己的错误,并同意做出改正.