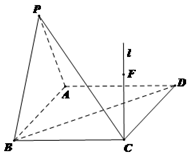
已知矩形\(ABCD\)满足\(AB=2\)，\(BC=\sqrt{2}\)，\(\triangle PAB\)是正三角形，平面\(PAB⊥\)平面\(ABCD.\)
\((1)\)求证：\(PC⊥BD\)；
\((2)\)设直线\(l\)过点\(C\)且\(l⊥\)平面\(ABCD\)，点\(F\)是直线\(l\)上的一个动点，且与点\(P\)位于平面\(ABCD\)的同侧，记直线\(PF\)与平面\(PAB\)所成的角为\(θ\)，若\(0< CF< 2\sqrt{3}\)，求\(\tan θ\)的取值范围．