如图，在四棱锥\(P-ABCD\)中，\(AD/\!/BC,\angle ADC=\angle PAB={{90}^{\circ }},BC=CD=\dfrac{1}{2}AD,E\)为棱\(AD\)的中点，异面直线\(PA\)与\(CD\)所成的角为\(\dfrac{\pi }{2}\)．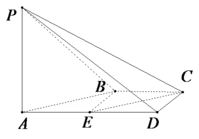

\((1)\)在平面\(PAB\)内找一点\(M\)，使得直线\(CM/\!/\)平面\(PBE\)，并说明理由．

\((2)\)若二面角\(P-CD-A\)的大小为\(\dfrac{\pi }{4}\)，求直线\(PA\)与平面\(PCE\)所成角的正弦值．