等边三角形\(ABC\)的边长为\(3\)，点\(D\)、\(E\)分别是边\(AB\)、\(AC\)上的点，且满足\( \dfrac{AD}{DB}= \dfrac{CE}{EA}= \dfrac{1}{2}(\)如图\(1).\)将\(\triangle ADE\)沿\(DE\)折起到\(\triangle A_{1}DE\)的位置，使二面角\(A_{1}-DE-B\)成直二面角，连接\(A_{1}\)B、\(A_{1}C(\)如图\(2)\)．
   
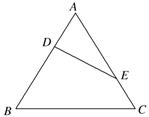
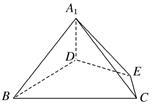
               图\(1\)                                 图\(2\)
\((1)\)求证：\(A\)\({\,\!}_{1}\)\(D⊥\)平面\(BCED\)；
\((2)\)在线段\(BC\)上是否存在点\(P\)，使直线\(PA\)\({\,\!}_{1}\)与平面\(A\)\({\,\!}_{1}\)\(BD\)所成的角为\(60^{\circ}\)？若存在，求出\(PB\)的长；若不存在，请说明理由．