\((1)\)若命题“\({∃}t{∈}R{,}t^{2}{-}2t{-}a{ < }0\)”是假命题，则实数\(a\)的取值范围是______

\((2)\)若\(\theta\)是任意实数，则方程\(x^{2}{+}y^{2}\sin\theta{=}4\)表示的曲线可能是______\({.}(\)填上所有可能的序号\(){①}\)椭圆 \({②}\)双曲线 \({③}\)抛物线  \({④}\)圆  \({⑤}\)直线  \({⑥}\)点\(.\)

\((3)\)点\(P\)在椭圆\(\dfrac{x^{2}}{16}{+}\dfrac{y^{2}}{9}{=}1\)上，则点\(P\)到直线\(3x{-}4y{=}24\)的最大距离和最小距离为______ ．

\((4)\)已知双曲线\(C\)：\(\dfrac{x^{2}}{a^{2}}{-}\dfrac{y^{2}}{b^{2}}{=}1(a{ > }0{,}b{ > }0)\)的右顶点为\(A\)，以\(A\)为圆心，\(b\)为半径作圆\(A\)，圆\(A\)与双曲线\(C\)的一条渐近线交于\(M\)、\(N\)两点\({.}\)若\({∠}{MAN}{=}60^{{∘}}\)，则\(C\)的离心率为______ ．

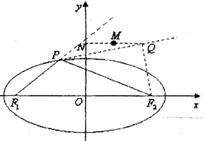
\((5)\)如图，已知椭圆\(\dfrac{x^{2}}{4}{+}y^{2}{=}1\)的焦点为\(F_{1}\)、\(F_{2}\)，点\(P\)为椭圆上任意一点，过\(F_{2}\)作\({∠}F_{1}PF_{2}\)的外角平分线的垂线，垂足为点\(Q\)，过点\(Q\)作\(y\)轴的垂线，垂足为\(N\)，线段\(QN\)的中点为\(M\)，则点\(M\)的轨迹方程为______ ．