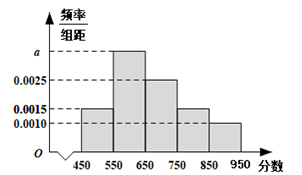某市为提高市民的安全意识，组织了一场知识竞赛，已知比赛共有\(2000\)位市民报名参加，其中男性\(1200\)人，现从参赛的市民当中采取分层抽样的方法随机抽取了\(100\)位市民进行调查，根据调查结果发现分数分布在\(450～950\)分之间，将结果绘制的市民分数频率分布直方图如图所示：
将分数不低于\(750\)分的得分者称为“高分选手”．
\((1)\)求\(a\)的值，并估计该市市民分数的平均数、中位数和众数\((\)同一组中的数据用该组区间的中点值作代表\()\)；
\((2)\)若样本中属于“高分选手”的女性有\(15\)人，完成下列\(2×2\)列联表，并判断是否有\(97.5％\)的把握认为该市市民属于“高分选手”与“性别”有关？

	属于“高分选手”	不属于“高分选手”	合计
男生
女生
合计

\((\)参考公式：\(K^{2}=\dfrac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}\)，其中\(n=a+b+c+d.)\)

\(P(K^{2}\geqslant k)\)	\(0.15\)	\(0.10\)	\(0.05\)	\(0.025\)	\(0.010\)	\(0.005\)	\(0.001\)
\(k\)	\(2.072\)	\(2.706\)	\(3.841\)	\(5.024\)	\(6.635\)	\(7.879\)	\(10.828\)