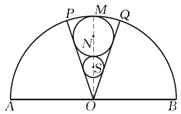如图，有一块半径为\(R\)的半圆形广场，\(M\)为\( \overparen {AB}\)的中点．现要在该广场内以\(OM\)为中轴线划出一块扇形区域\(OPQ\)，并在扇形区域内建两个圆形花圃\((\)圆\(N\)和圆\(S)\)，使得圆\(N\)内切于扇形\(OPQ\)，圆\(S\)与扇形\(OPQ\)的两条半径相切，且与圆\(N\)外切．记\(∠POM=θ( 0 < θ < \dfrac {π}{2} )\)，则圆\(S\)的半径\(y\)可表示成\(θ\)的函数式为______，圆\(S\)的半径\(y\)的最大值为______．