如图，已知抛物线\(C:y^{2}=2px(p>0)\)的焦点为\(F\)，过点\(F\)的直线\(l\)与抛物线交于\(AB\)两点，且\(\left|AB\right|\)的最小值为\(4.\)

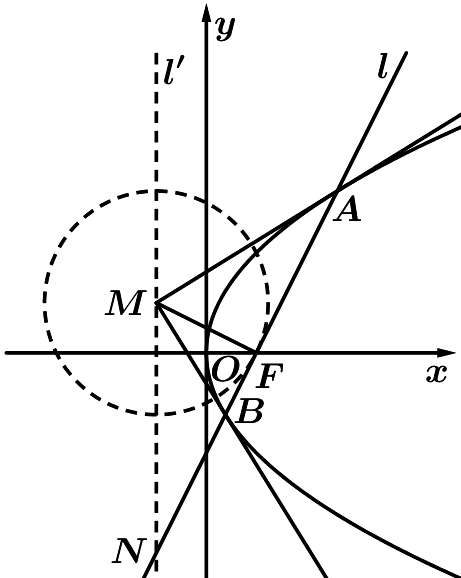
\((1)\)求抛物线\(C\)的方程\(;\)
\((2)\)过\(A\)、\(B\)分别作抛物线\(C\)的切线，两切线交于点\(M.\)
①求证：以\(M\)为圆心，\(MF\)为半径的圆恰与直线\(l\)相切\(;\)

②设直线\(l\)与准线\({l}^{'}\)交于点\(N\)，若\(\left|MN\right|=\left|AB\right|\)，求直线\(l\)的方程.