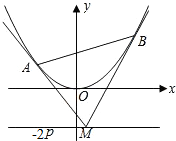
如图，设抛物线方程为\(x ^{2} =2py(p > 0)\)，\(M\)为直线\(y=-2p\)上任意一点，过\(M\)引抛物线的切线，切点分别为\(A\)，\(B\)．
\((\)Ⅰ\()\)设线段\(AB\)的中点为\(N\)；
\((ⅰ)\)求证：\(MN\)平行于\(y\)轴；
\((ⅱ)\)已知当\(M\)点的坐标为\((2 , -2p)\)时，\(|AB|=4 \sqrt {10}\)，求此时抛物线的方程；
\((\)Ⅱ\()\)是否存在点\(M\)，使得点\(C\)关于直线\(AB\)的对称点\(D\)在抛物线\(x ^{2} =2py(p > 0)\)上，其中，点\(C\)满足\( \overrightarrow {OC}= \overrightarrow {OA}+ \overrightarrow {OB} (O\)为坐标原点\().\)若存在，求出所有适合题意的点\(M\)的坐标；若不存在，请说明理由．