题型：选择题 题类：其他 难易度：中档
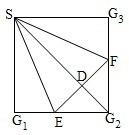在正方形\(SG_{1}G_{2}G_{3}\)中，\(E\)、\(F\)分别是\(G_{1}G_{2}\)及\(G_{2}G_{3}\)的中点，\(D\)是\(EF\)的中点，现在沿\(SE\)、\(SF\)及\(EF\)把这个正方形折成一个四面体，使\(G_{1}\)、\(G_{2}\)、\(G_{3}\)三点重合，重合后的点记为\(G\)，那么，在四面体\(S-EFG\)中必有\((\) \()\) 