山东省2021年普通高校招生(春季）考试数学真题-试卷

选择本卷全部试题

题型：选择题难易度：易

1 . (2021•山东)已知集合U={ 0，1，2，3，4 }，集合 M={ 1，2，3 }，N={ 2，4 }，则 M∩(\( {C}_{U}N\))等于 (　　)

A. { 2 } B. { 1，3 } C. { 0，1，3 } D. { 0，1，2，3 }

查看解析收藏纠错

+选题
题型：选择题难易度：易

2 . (2021•山东)函数\( y=\sqrt{|x-1|-3}\)的定义域是 (　　)

A. (-2，4) B. (-∞，-2)∪(4，+∞) C. [-2，4] D. (-∞，-2)∪[4，+∞)

查看解析收藏纠错

+选题
题型：选择题难易度：中档

3 . (2021•山东)已知函数f(x) 在 (-∞，+∞) 上是减函数，则下列关系正确的是 (　　)

A. f (1) B. f(0)≤f(-1) C. f(-1) D. f(0)

查看解析收藏纠错

+选题
题型：选择题难易度：中档

4 . (2021•山东)已知函数y=log_ax (a>0且a≠1)的图像如图所示，则函数y=(1-a)x²+1的图像大致是 (　　)

A. B. C. D.

查看解析收藏纠错

+选题
题型：选择题难易度：中档

5 . (2021•山东)下列命题正确的是 (　　)

A. 零向量没有方向 B. 两个单位向量相等 C. 方向相反的两个向量互为相反向量 D. 若\( \overrightarrow{AB}//\overrightarrow{AC}\), 则 A，B，C 三点共线

查看解析收藏纠错

+选题
题型：选择题难易度：中档

6 . (2021•山东)角α的顶点在坐标原点，始边与x轴非负半轴重合，终边过点P (-1，2)，则sin2a等于 (　　)

A. \( -\frac{3}{5}\) B. \( \frac{3}{5}\) C. \( -\frac{4}{5}\) D. \( \frac{4}{5}\)

查看解析收藏纠错

+选题
题型：选择题难易度：易

7 . (2021•山东) “角α是第一象限角"是"sinα≥0"的 (　　)

A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件

查看解析收藏纠错

+选题
题型：选择题难易度：中档

8 . (2021•山东)如图所示，已知直线\( m\perp l\)，则直线m的方程为 (　　)

A. x-2y-1=0 B. x-2y+1=0 C. 2x-y-5=0 D. 2x-y+5=0

查看解析收藏纠错

+选题
题型：选择题难易度：中档

9 . (2021•山东)某运动队准备参加4×100米接力赛，队中共有5名运动员，其中甲运动员不能跑第一棒，教练从这5人中安排4人分别跑第一至第四棒 ,则所有不同安排方法的种数是 (　　)

A. 48 B. 60 C. 96 D. 120

查看解析收藏纠错

+选题
题型：选择题难易度：易

10 . (2021•山东)已知函数f(x)的对应值如下表所示：
函数y=f(x)的对应值表

x 0 1 2 3 4 5

y 3 6 5 4 2 7

则f[f(2)]等于 (　　)

A. 4 B. 5 C. 6 D. 7

查看解析收藏纠错

+选题
题型：选择题难易度：中档

11 . (2021•山东)已知向量a=(-2，3 )，b ( m，1 )，若ab=5，则实数m的值是 (　　)

A. -1 B. -4 C. \( \frac{3}{2}\) D. \( \frac{7}{3}\)

查看解析收藏纠错

+选题
题型：选择题难易度：中档

12 . (2021•山东)函数\( y=A\mathit{sin}(\omega x+\phi \left)\right(A>0,\omega >0,\left|\phi \right|<\frac{\pi }{2})\)的部分图，像如图所示，则下列说法正确的是 (　　)

A. 该函数为偶函数 B. 该函数的最大值为1 C. 该函数的最小正周期是4π D. φ的值是\( -\frac{\pi }{3}\)

查看解析收藏纠错

+选题
题型：选择题难易度：难

13 . (2021•山东)在幼儿园 "体验分享，快乐成长" 的活动中，有三位小朋友都把自己的一件玩具交给老师，老师再把这三件玩具随机发给他们，每人一件，则这三位小朋友都没有拿到自己玩具的概率是 (　　)

A. \( \frac{1}{2}\) B. \( \frac{1}{3}\) C. \( \frac{1}{4}\) D. \( \frac{1}{6}\)

查看解析收藏纠错

+选题
题型：选择题难易度：中档

14 . (2021•山东)已知过原点的圆，其圆心坐标为 ( 1，2 )，则该圆的标准方程为 (　　)

A. (x-1)²+(y-2)²=5 B. (x-1)²+(y-2)²=4 C. (x+1)²+(y+2)²=5 D. (x+1)²+(y+2)²=4

查看解析收藏纠错

+选题
题型：选择题难易度：难

15 . (2021•山东)已知点M在抛物线y²=2px(p>0)上，若点M到抛物线对称轴的距离是4，到准线的距离是5，则p的值是 (　　)

A. 2或4 B. 4或6 C. 6或8 D. 2或8

查看解析收藏纠错

+选题
题型：选择题难易度：易

16 . (2021•山东)已知命题 ρ：甲、乙、丙三名同学都是共青团员，则-p为 (　　)

A. 甲、乙、丙三名同学都不是共青团员 B. 甲、乙、丙三名同学中至少有一名不是共青团员 C. 甲、乙、丙三名同学中至少有两名不是共青团员 D. 甲、乙、丙三名同学中至多有一名不是共青团员

查看解析收藏纠错

+选题
题型：选择题难易度：易

17 . (2021•山东)在下列不等式中，能表示如图所示区域 (阴影部分) 的是 (　　)

A. x+3y-3<0 B. x+3y-3>0 C. x+3y-3≤0 D. x+3y-3≥0

查看解析收藏纠错

+选题
题型：选择题难易度：难

18 . (2021•山东)在《九章算术》中有如下问题："有甲、乙、丙、丁、戊五人分30斤小米，其中甲、乙两人所分小米的斤数之和与丙、丁、戊三人所分小米的斤数之和相等，且甲、乙、丙、丁、戊五人所分小米的斤数依次成等差数列，问每人各分多少斤." 那么，甲所分小米的斤数是 (　　)

A. 6 B. 7 C. 8 D. 9

查看解析收藏纠错

+选题
题型：选择题难易度：中档

19 . (2021•山东)在\( (\frac{1}{x}-2{)}^{n}\)的展开式中，若第2项与第5项的二项式系数相等，则第4项的系数是 (　　)

A. -10 B. -80 C. 40 D. 560

查看解析收藏纠错

+选题
题型：选择题难易度：难

20 . (2021•山东)如图所示，在正方体 ABCD-\( {A}_{1}{B}_{1}{C}_{1}{D}_{1}\)中，E，F 分别是\( {A}_{1}{B}_{1}，{A}_{1}{D}_{1}\)的中点.若P为线段 BD上的动点，则下列结论中，正确的是 (　　)

A. PC₁∥AE B. PC₁⊥A₁C C. PC₁∥平面AEF D. PC₁⊥平面 BB₁D₁D

查看解析收藏纠错

+选题
题型：填空题难易度：易

21 . (2021•山东)函数y=2sinx-3的最大值是______。

查看解析收藏纠错

+选题
题型：填空题难易度：

22 . (2021•山东)已知正四棱锥的底面边长为1，侧棱长为2，则该正四棱锥的表面积等于______。

查看解析收藏纠错

+选题
题型：填空题难易度：易

23 . (2021•山东)已知椭圆的长轴长与短轴长的比是 3∶2，则该椭圆的离心率是______。

查看解析收藏纠错

+选题
题型：填空题难易度：

24 . (2021•山东)某同学 6 次技能测试的成绩分别是 85，91，88，87，90，87，为了精确评价该同学技能发挥的稳定性，通过数据分析得到该组数据的标准差是______。

查看解析收藏纠错

+选题
题型：填空题难易度：难

25 . (2021•山东)已知点A，B，C在函数y=3^x的图像上，这三个点的横坐标依次构成公差为1的等差数列。若点A的横坐标为m，△ABC的面积为S，把S表示为以m为自变量的函数，则该函数的解析式是______。

查看解析收藏纠错

+选题
题型：解答题难易度：易

26 . (2021•山东) (本小题7分) 已知f(x)是定义在R上的奇函数，当x≥0时，f(x)=ax²-2x，且f(4)=8。求：
(1)实数a的值；
(2) 该函数的解析式。

查看解析收藏纠错

+选题
题型：解答题难易度：

27 . (2021•山东) (本小题8分) 在数列{a_n}中，a_n≥0，a₁=1，2a+1-an=0。
(1)求数列{a_n}的通项公式：
(2)若b_n=loga_n, 求数列{b_n}的前90项和S₉₀。

查看解析收藏纠错

+选题
题型：解答题难易度：难

28 . (2021•山东) (本小题8分) 如图所示，已知∠POQ=30°点A在OP上，OA=10，以点A为圆心，半径为\( 5\sqrt{2}\)的圆与OQ相交于B，C，且OB≥OC。
(1)求∠OBA 的大小；
(2)若D为OA的中点，求线段CD的长。(精确到0.1 )

查看解析收藏纠错

+选题
题型：解答题难易度：难

29 . (2021•山东) (本小题8分) 在四棱锥S-ABCD中，已知底面ABCD是正方形，SA⊥面ABCD，∠SDA= 60 °，如图所示。
(1)求证AB⊥SD；
(2)若E，F分别是AB，SC的中点，求直线EF与AD所成角的大小。

查看解析收藏纠错

+选题
题型：解答题难易度：难

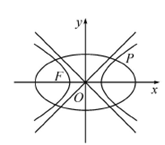
30 . (2021•山东) (本小题9分)如图所示，已知双曲线，\( \frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)\)的左顶点与椭圆\( \frac{{x}^{2}}{5}+\frac{{y}^{2}}{4}=1\)的左焦点F重合.双曲线与椭圆在第一象限相交于点\( P(\frac{5}{3},\frac{4}{3})\)。
(1)求双曲线的标准方程 ;
(2)过点F的直线\( l\)与椭圆相交于点M，N，线段MN的中点在双曲线的渐近线上，求直线\( l\)的方程。

查看解析收藏纠错

+选题
下载word版试卷(含答案解析)

高中

山东省2021年普通高校招生(春季）考试数学真题

试卷分析

服务介绍

帮助中心

高中

山东省2021年普通高校招生(春季）考试 数学真题

试卷分析

服务介绍

帮助中心

山东省2021年普通高校招生(春季）考试数学真题