第四章三角函数-山东版高教版（上册）数学同步练习题

选择章节

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：389 选择本页全部试题

题型：解答题题类：其他难易度：中档

年份：2018

\((\)Ⅰ\()\) 化简：；

\((\)Ⅱ\()\)已知\(α\)为第二象限的角，化简：．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：中档

年份：2018

已知\(0 < \alpha < \dfrac{\pi }{2},\sin \alpha =\dfrac{4}{5}\)
\((1)\)求\(\tan \alpha \)的值；

\((2)\)求\(\dfrac{\sin (\alpha +\pi )-2\cos (\dfrac{\pi }{2}+\alpha )}{-\sin (-\alpha )+\cos (\pi +\alpha )}\)的值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：模拟题难易度：中档

年份：2018

在平面四边形中，\(∠ADC={90}^{∘} \)，\(∠A={45}^{∘} \)，\(AB=2 \)，\(BD=5 \)．

\((1)\)求\(\cos ⁡∠ADB \)；

\((2)\)若\(DC=2 \sqrt{2} \)，求\(BC \)．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：中档

年份：2018

已知\(f(x)\)是定义在\((-1,1)\)上的奇函数．

\((1)\)若\(f(x)\)在\((-1,1)\)上单调递减，且\(f(1-a)+f(1-2a) < 0\)，求实数\(a\)的取值范围；

\((2)\)当\(0 < x < 1\)时，\(f(x)={{x}^{2}}+x+1\)，求\(f(x)\)在\((-1,1)\)上的解析式．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：中档

年份：2018

已知函数\(f(x)=2\sin x\cdot \cos x-{{\cos }^{2}}x+{{\sin }^{2}}x\)，\(x∈R \)．

\((\)Ⅰ\()\)求\(f(x)\)的最小正周期及单调递减区间；

\((\)Ⅱ\()\)求\(f(x)\)在区间\([0. \dfrac{π}{2}] \)上的最大值和最小值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：中档

年份：2018

已知\({\triangle }ABC\)中，内角\(A\)，\(B\)，\(C\)的对边分别为\(a\)，\(b\)，\(c\)，若\((2a{-}c)\cos B{=}b\cos C\)．
\((1)\)求角\(B\)的大小；
\((2)\)若\(b{=}2\)，求\({\triangle }ABC\)周长的最大值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：期中考试难易度：中档

年份：2018

已知\(\cos θ= \dfrac{12}{13},θ∈\left(π,2π\right) \)，求\(\sin \left( \left. θ- \dfrac{π}{6} \right. \right)\)以及\(\tan \left( \left. θ+ \dfrac{π}{4} \right. \right)\)的值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：中档

年份：2018

设\(\triangle ABC\)中的内角\(A\)、\(B\)、\(C\)所对的边长分别为\(a\)，\(b\)，\(c\)，且\(\cos B=\dfrac{4}{5}\)，\(b=2\)。

\((1)\)求当\(a=\dfrac{5}{3}\)时，求\(A\)；

\((2)\)求\(\triangle ABC\)面积的最大值。

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：中档

年份：2018

已知\(A(x_{A},y_{A})\)是单位圆\((\)圆心为坐标原点\(O\)，半径为\(1)\)上任意一点，将射线\(OA\)绕点\(O\)逆时针旋转\(\dfrac{\pi}{6}\)到\(OB\)交单位圆于点\(B(x_{B},y_{B})\)，已知\(m > 0\)，若\(my_{A}-2y_{B}\)的最大值为\(2\)，求实数\(m\)的值．

查看解析收藏纠错相似题

+选题
题型：解答题题类：其他难易度：中档

年份：2018

如图，在一条海防警戒线上的点\(A\)、\(B\)、\(C\)处各有一个水声监测点，\(B\)、\(C\)两点到\(A\)的距离分别为\(20\)千米和\(50\)千米，某时刻，\(B\)收到发自静止目标\(P\)的一个声波信号，\(8\)秒后\(A\)、\(C\)同时接到该声波信号，已知声波在水中的传播速度是\(1.5\)千米\(/\)秒．

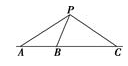
\((1)\)设\(A\)到\(P\)的距离为\(x\)千米，用\(x\)表示\(B\)、\(C\)到\(P\)的距离，并求\(x\)的值；

\((2)\)求\(P\)到海防警戒线\(AC\)的距离．

查看解析收藏纠错相似题

+选题

高中

选择章节

服务介绍

帮助中心