题型：解答题 题类：期末考试 难易度：易
新年份：2020
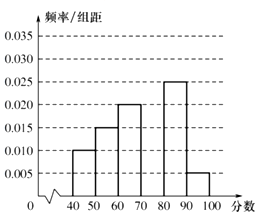某校为了解疫情期间学生线上学习效果，进行一次摸底考试，从中选取\(60\)名同学的成绩\((\)百分制，均为正数\()\)分成\([40 , 50)\)，\([50 , 60)\)，\([60 , 70)\)，\([70 , 80)\)，\([80 , 90)\)，\([90 , 100)\)六组后，得到部分频率分布直方图\((\)如图\()\)，观察图形，回答下列问题：题型：解答题 题类：期末考试 难易度：易
新年份：2020
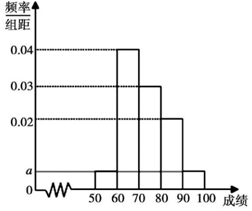某校为了解高一年级学生的数学学科发展状况，随机抽取了\(100\)名学生，列出他们的高一第二学期期中考试数学成绩的频率分布直方图如图，其中成绩的分组区间为：\([50 , 60)\)，\([60 , 70)\)，\([70 , 80)\)，\([80 , 90)\)，\([90 , 100]\)．