题型：选择题 题类：期末考试 难易度：较难
测年份：2018
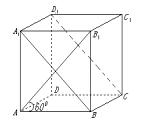
如图，四棱柱\(ABCD-{A}_{1}{B}_{1}{C}_{1}{D}_{1} \)中，底面为正方形，侧棱垂直于底面，底面边长为\(1\)，\(A{B}_{1} \)与底面\(ABCD\)成\(60^{\circ}\)角，则\(A{{B}_{1}}\)与平面\({{A}_{1}}BC{{D}_{1}}\)所成的角为\((\) \()\)
题型：选择题 题类：期末考试 难易度：较难
测年份：2018
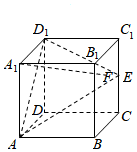在正方体\(ABCD-A_{1}B_{1}C_{1}D_{1}\)中，\(E\)是棱\(CC_{1}\)的中点，\(F\)是侧面\(BCC_{1}B_{1}\)内的动点，且\(A_{1}F/\!/\)平面\(D_{1}AE\)，则\(A_{1}F\)与平面\(BCC_{1}B_{1}\)所成角的正切值\(t\)构成的集合是\((\) \()\) 
如图，在矩形ABCD中，AB=2，BC=1，E、N分别为边AB，BC的中点，沿DE将△ADE折起，点A折至A1处（A1与A不重合），若M、K分别为线段A1D，A1C的中点，则在MDE折起过程中，（ ） 
正四面体ABCD中，CD在平面α内，点E是线段AC的中点，在该四面体绕CD旋转的过程中，直线BE与平面α所成角的余弦值不可能是（ ） 
