题型：解答题 题类：期中考试 难易度：中档
年份：2018
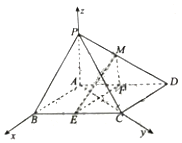在四棱锥\(P-ABCD\)中，底面\(ABCD\)是平行四边形，侧棱\(PA⊥\)底面\(ABCD\)，\(AB⊥AC\)，\(AB=AC=PA=2\)，\(E\)，\(F\)分别为\(BC\)，\(AD\)的中点，点\(M\)在线段\(PD\)上，以\(AB\)，\(AC\)，\(AP\)分别为\(x\)轴、\(y\)轴、\(z\)轴，如图建立空间直角坐标系．题型：解答题 题类：期中考试 难易度：中档
年份：2018
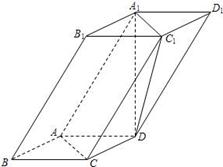
如图，四棱柱\(ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\)中，\({{A}_{1}}D\bot \)平面\(ABCD\)，底面\(ABCD\)是边长为\(1\)的正方形，侧棱\(A{{A}_{1}}=2\)．
题型：解答题 题类：期中考试 难易度：中档
年份：2018
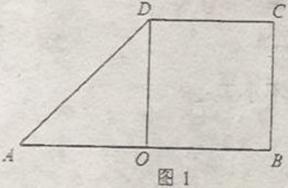
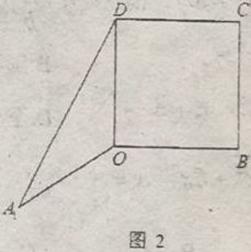
如图\(1\)，在梯形\(ABCD\)中，\(AB/\!/CD\)，\(∠ABC=90^{\circ}\)，\(AB=2CD=2BC=4\)，\(O\)是边\(AB\)的中点，将三角形\(AOD\)绕边\(OD\)所在直线旋转到\(A_{1}OD\)位置，使得\(∠A_{1}OB=120^{\circ}\)，如图\(2\)，设\(m\)为平面\(A_{1}DC\)与平面\(A_{1}OB\)的交线．
\((1)\)判断直线\(DC\)与直线\(m\)的位置关系并证明；
\((2)\)若直线\(m\)上的点\(G\)满足\(OG⊥A_{1}D\)，求山\(A_{1}G\)的长；
\((3)\)求直线\(A_{1}O\)与平面\(A_{1}BD\)所成角的正弦值．
如图，在边长为2的菱形ABCD中，∠ABC=60°，PC⊥面ABCD，E，F是PA和AB的中点．
如图所示，在长方体\(ABCDA_{1}B_{1}C_{1}D_{1}\)中，\(AD=CD=4\)，\(AD_{1}=5\)，\(M\)是\(B_{1}D_{1}\)的中点．
，求AD的长．
