代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：42选择本页全部试题

题型：填空题题类：期中考试难易度：难
新
年份：2020

已知函数\(f(x)=a\boldsymbol{⋅}2 ^{x} +b\)的图象过点\((2 , 9)\)和点\((4 , 45)\)，若数列\(\{a _{n} \}\)的前\(n\)项和\(S _{n} =f(n)\)，数列\(\{ \log _{2}\dfrac{a_{n}}{3}\}\)的前\(n\)项和为\(T _{n}\)，则使得\(T _{n} \geqslant 55\)成立的最小正整数\(n=\)______．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：难
新
年份：2020

用\(n\)种不同颜色为下侧两块广告牌着色\((\)如图甲、乙所示\()\)，要求在①、②、③、④四个区域中相邻\((\)有公共边界\()\)的区域不用同一种颜色．
\((1)\)若\(n=6\)，为甲着色时共有多少种不同方法？
\((2)\)若为乙着色时共有\(120\)种不同方法，求\(n\)．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：难
新
年份：2020

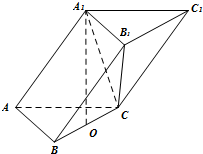在三棱柱\(ABC-A _{1} B _{1} C _{1}\)中，已知\(AB=AC=AA _{1} = \sqrt {5}\)，\(BC=4\)，点\(A _{1}\)在底面\(ABC\)的投影是线段\(BC\)的中点\(O\)．
\((1)\)证明在侧棱\(AA _{1}\)上存在一点\(E\)，使得\(OE⊥\)平面\(BB _{1} C _{1} C\)，并求出\(AE\)的长；
\((2)\)求平面\(A _{1} B _{1} C\)与平面\(BB _{1} C _{1} C\)夹角的余弦值．

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：难
新
年份：2020

定义函数\(f(x)=(1-x ^{2} )(x ^{2} +bx+c)\)．
\((1)\)如果\(f(x)\)的图象关于\(x=2\)对称，求\(2b+c\)的值；
\((2)\)若\(x∈[-1 , 1]\)，记\(|f(x)|\)的最大值为\(M(b , c)\)，当\(b\)、\(c\)变化时，求\(M(b , c)\)的最小值．

查看解析收藏纠错

+选题
题型：选择题题类：期中考试难易度：难
新测
年份：2020

在\(\triangle ABC\)中，若\((a+b+c)(b+c-a)=3bc\)，且\(\sin A=2\sin B\cos C\)，则\(\triangle ABC\)的形状是\((\:\:\:\:)\)

A.直角三角形 B.等腰直角三角形 C.等腰三角形 D.等边三角形

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：难
新
年份：2020

在\(\triangle ABC\)中，\(BC=a\)，\(AC=b\)，\(a\)，\(b\)是方程\({{x}^{2}}-2\sqrt{3}x+2=0\)的两个根，且\(2\cos (A+B)=1\)。
求：\((1)\)角\(C\)的度数；
\((2)AB\)的长度。

查看解析收藏纠错

+选题
题型：解答题题类：期中考试难易度：难
新
年份：2020

将圆心角为\(120°\)，面积为\(3π\)的扇形，作为圆锥的侧面，求圆锥的表面积和体积．

查看解析收藏纠错

+选题
题型：填空题题类：期中考试难易度：难
新
年份：2020

已知点\(A(2 , 3)\)，\(B(-3 , -2)\)，若直线\(l\)过点\(P(1 , 1)\)与线段\(AB\)相交，则直线\(l\)的斜率\(k\)的取值范围是 ______ ．

查看解析收藏纠错

+选题
题型：填空题题类：期中考试难易度：难
新
年份：2020

设\(F\)为抛物线\(y ^{2} =4x\)的焦点，\(A\)，\(B\)，\(C\)为该抛物线上三点，若\( \overrightarrow {FA}+ \overrightarrow {FB}+ \overrightarrow {FC}= \overrightarrow {0}\)，则\(| \overrightarrow {FA}|+| \overrightarrow {FB}|+| \overrightarrow {FC}| =\)______．

查看解析收藏纠错

+选题
题型：选择题题类：期中考试难易度：难
新测
年份：2020

已知变量\(x\)，\(y\)满足\(\begin{cases}x-2y+4\leqslant0,\\x\geqslant2\\x+y-6\geqslant0\end{cases}\)，则\(k= \dfrac {y+1}{x-3}\)的取值范围是\((\:\:\:\:)\)

A.\(k > \dfrac {1}{2}\)或\(k\leqslant -5\) B.\(-5\leqslant k < \dfrac {1}{2}\) C.\(-5\leqslant k\leqslant \dfrac {1}{2}\) D.\(k\geqslant \dfrac {1}{2}\)或\(k\leqslant -5\)

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心