题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)若函数\(f\left( x \right){=}kx{-}\ln x\)在区间\(\left( 1{,+∞} \right)\)上单调递增,则\(k\)的取值范围是__________.
\((2)\)若直线\(x{-}y{-}2{=}0\)被圆\(x^{2}{+}{(y{+}a)}^{2}{=}4\)所截得的弦长为\(2\sqrt{2}\),则实数\(a\)的值为____.
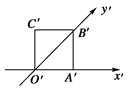
\((3)\)如图,正方形\(O^{{{{{'}}}}}A^{{{{{'}}}}}B^{{{{{'}}}}}C^{{{{{'}}}}}\)的边长为\({acm}\left( a{ > }0 \right)\),它是一个水平放置的平面图形的直观图,则它的原图形\({OABC}\)的周长是___________\({cm}\).
\((4)\)下列说法中不正确的是________\(.(\)填序号\()\)
\(①\)若\(a∈R\),则“\(\dfrac{1}{a} < 1\)”是“\(a > 1\)”的必要不充分条件;
\(②\)“\(p∧q\)为真命题”是“\(p∨q\)为真命题”的必要不充分条件;
\(③\)若命题\(p\):“\(∀x∈R\),\(\sin x+\cos x\leqslant \sqrt{2}\)”,则\(p\)是真命题;
\(④\)命题“\(∃x_{0}∈R\),\(x_{0}^{2}+2x_{0}+3 < 0\)”的否定是“\(∀x∈R\),\(x^{2}+2x+3 > 0\)”.
题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)计算\({\log }_{3}2×{\log }_{4}27 \)____________。
\((2)\)已知两点\(A(1,0)\)、\(B(0,2)\),点\(P\)是圆\((x+1{)}^{2}+{y}^{2}=1 \)上任意一点,则\(\triangle PAB \)的面积的最小值为______。
\((3)\)已知角\(α \)的终边经过点\(P(2,m)(m\neq 0 )\),若\(\sin α= \dfrac{ \sqrt{5}}{5}m \),则\(\sin (2α+ \dfrac{3π}{2}) \)____________。
\((4)\)以等腰直角三角形\(ABC\)的斜边\(BC\)上的中线\(AD\)为折痕,将\(\triangle ABD \)与\(\triangle ACD \)折成互相垂直的两个平面,得到以下四个结论:\(①BD⊥ \)平面\(acd;②\triangle ABC \)为等边三角形\(;③\)平面\(ADC⊥ \)平面\(ABC\);\(④\)点\(D\)在平面\(ABC\)内的射影为\(\triangle ABC \)的外接圆圆心。其中正确的命题有____________。\((\)填上所有正确的命题序号\()\)