题型：选择题 题类：期末考试 难易度：较易
新 测年份：2021
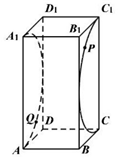如图，已知正四棱柱\(ABCD-A_{1}B_{1}C_{1}D_{1}\)的底面边长为\(1\)，侧棱长为\(2\)，点\(P\)，\(Q\)分别在半圆弧\(\hat{C}_{1}C\)，\(\hat{A}_{1}A(\)均不含端点\()\)上，且\(C_{1}\)，\(P\)，\(Q\)，\(C\)在球\(O\)上，则\((\quad)\) 题型：填空题 题类：期末考试 难易度：较易
新年份：2021
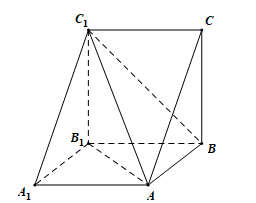《九章算术》中记载：将底面为直角三角形的直三棱柱称为堑堵，将一堑堵沿其一顶点与相对的棱剖开，得到一个阳马\((\)底面是长方形，且有一条侧棱与底面垂直的四棱锥\()\)和一个鳖臑\((\)四个面均为直角三角形的四面体\()\)在如图所示的堑堵\(ABC-A_{1}B_{1}C_{1}\)中，\(BB_{1}=BC=AB=2\)且有鳖臑\(C_{1}-ABB_{1}\)和鳖臑\(C_{1}-ABC\)，现将鳖臑\(C_{1}-ABC\)的一个面\(ABC_{1}\)沿\(BC_{1}\)翻折\(180°\)，使\(A\)点翻折到\(E\)点，求形成的新三棱锥\(C_{1}-AB_{1}E\)的外接球的表面积是 ______. 
如图，已知边长为\(4\)的菱形\(ABCD\)中，\(∠ABC=60°\)，将\(\triangle ABC\)沿对角线\(AC\)翻折至\(\triangle AB'C\)所在的位置，若二面角\(B'-AC-D\)的大小为\(120°\)，则过\(A\)，\(B'\)，\(C\)，\(D\)四点的外接球的表面积为 ______. 
正方形\(ABCD\)的边长是\(4\)，点\(E\)、\(F\)分别是\(AB\)、\(BC\)的中点，现将\(\triangle ADE\)，\(\triangle EBF\)，\(\triangle FCD\)分别沿\(DE\)，\(EF\)，\(FD\)折起，使得\(A\)、\(B\)、\(C\)三点重合于一点\(A'.\)若四面体\(A'EFD\)的四个顶点在同一个球面上，则该球的表面积为 ______. 