题型:选择题 题类:其他 难易度:较难
测年份:2018
如图,棱长为\(4\)的正方体\(ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\)中,点\(E\)为棱\(BC\)的中点,点\(M\)为平面\({{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\)上任意一点,点\(P\)为线段\({{A}_{1}}B\)上的任意一点,点\(N\)为平面\(ABCD\)上一动点,且点\(N\)满足到点\(A\)的距离等于到直线\(DC\)的距离,则下列结论正确个数是
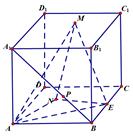
\(④\angle AP{{D}_{1}}\)的最大值为\(\dfrac{\pi }{2}\);\(⑤\)三棱锥\(N-AME\)体积的最大值为\(\dfrac{16}{3}\).
题型:选择题 题类:其他 难易度:较难
测年份:2018
已知三棱柱\(ABC-A_{1}B_{1}C_{1}\),平面\(β\)截此三棱柱,分别与\(AC\),\(BC\),\(B_{1}C_{1}\),\(A_{1}C_{1}\)交于点\(E\),\(F\),\(G\),\(H\),且直线\(CC_{1}/\!/\)平面\(β.\)有下列三个命题:\(①\)四边形\(EFGH\)是平行四边形;\(②\)平面\(β/\!/\)平面\(ABB_{1}A_{1}\);\(③\)若三棱柱\(ABC—A_{1}B_{1}C_{1}\)是直三棱柱,则平面\(β\)上平面\(A_{1}B_{1}C_{1}.\)其中正确的命题为
题型:选择题 题类:其他 难易度:较难
测年份:2018
\(E\)是正方体\(ABCD-{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}\)的棱\({{C}_{1}}{{D}_{1}}\)上的一点\((\)不与端点重合\()\),\(B{{D}_{1}}/\!/\)平面\({{B}_{1}}CE\),则 \((\) \()\)
题型:选择题 题类:其他 难易度:较难
测年份:2018
在直三棱柱\(ABC—A_{1}B_{1}C_{1}\)中,平面\(α\)与棱\(AB\),\(AC\),\(A_{1}C_{1}\),\(A_{1}B_{1}\)分别交于点\(E\),\(F\),\(G\),\(H\),且直线\(AA_{1}/\!/\)平面\(α.\)有下列三个命题:\(①\)四边形\(EFGH\)是平行四边形;\(②\)平面\(α/\!/\)平面\(BCC_{1}B_{1}\);\(③\)平面\(α⊥\)平面\(BCFE.\)其中正确的命题有
题型:选择题 题类:其他 难易度:较难
测年份:2018
设\(m\)、\(n\)是两条不同的直线,\(α\)、\(β\)是两个不同的平面,考查下列结论,其中正确的是( )
题型:选择题 题类:其他 难易度:较难
测年份:2018
如图,在三棱柱\(ABC-A_{1}B_{1}C_{1}\)中,侧棱\(AA_{1}⊥\)底面\(ABC\),\(AA_{1}=2\),\(AB=BC=1\),\(∠ABC=90^{\circ}\),外接球的球心为\(O\),点\(E\)是侧棱\(BB_{1}\)上的一个动点\(.\)有下列判断:
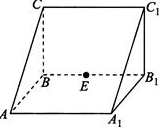
\(①\)直线\(AC\)与直线\(C_{1}E\)是异面直线;\(②A_{1}E\)一定不垂直于\(AC_{1}\);\(③\)三棱锥\(E-AA_{1}O\)的体积为定值;\(④AE+EC_{1}\)的最小值为\({2}\sqrt{{2}}\).
其中正确的个数是