题型：解答题 题类：模拟题 难易度：难
新年份：2019
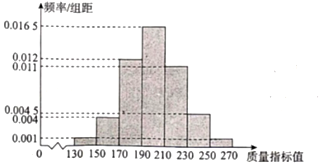某高科技公司投人1000万元研发某种产品，大规模投产后，每天在产品进入库房前，都需做严格的质量检验．为此，检验人员从当天生产的产品中随机抽取80件，检测一项关键的质量指标值（记为X），由检测结果得到如下样本频率分布直方图．
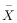、方差s2（同一组数据用该区间的中点值作代表）可作为μ，σ2的估计值．利用该正态分布，求P（X＞175.5）（精确到0.01）；
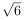≈2.45，P（μ-σ＜X≤μ+σ）=0.683，P（μ-2σ＜X≤μ+2σ）=0.954 题型：解答题 题类：模拟题 难易度：难
新年份：2019
,且与定直线
相切．
求动圆圆心C的轨迹E的方程； 
过点
的任一条直线l与轨迹E交于不同的两点P,Q,试探究在x轴上是否存在定点
异于点
,使得
？若存在,求点N的坐标；若不存在,说明理由． 
，x∈[0，π]，设f（x）的最大值为M，记f（x）取得最大值时x的值为θ．
，b=2
，B=θ，求c的值． 
．
，0＜θ＜π，求cosθ；
B,C,D在同一水平面内
,求A,D之间的距离． 
cosB）=0．
，c=
已知抛物线G的顶点在原点，焦点在y轴正半轴上，点P（m，4）到其准线的距离等于5．