代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：4214选择本页全部试题

题型：选择题题类：历年真题难易度：易
新测
年份：2019

已知集合M==（　　）

A.（-1，1）∪（1，2） B.（-1，2） C.（-1，1）∪（1，2] D.（-1，2]

查看解析收藏纠错

+选题
题型：填空题题类：历年真题难易度：易
新
年份：2019

（2x+y）（x-2y）⁵展开式中x³y³的系数为______．

查看解析收藏纠错

+选题
题型：填空题题类：历年真题难易度：较易
新
年份：2019

已知椭圆的左、右焦点分别为F₁，F₂，过左焦点F₁作斜率为－2的直线与椭圆交于A，B两点，P是AB的中点，O为坐标原点，若直线OP的斜率为，则a的值是_______________．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：中档
新
年份：2019

随着快递行业的崛起，中国快递业务量惊人，2018年中国快递量世界第一，已连续五年突破五百亿件，完全超越美日欧的总和，稳居世界第一名．某快递公司收取费的标准是：不超过1kg的包裹收费8元；超过1kg的包裹，在8元的基础上，每超过1kg（不足1kg，按1kg计算）需再收4元．
该公司将最近承揽（接收并发送）的100件包裹的质量及件数统计如下（表1）：
表1：
包裹重量（单位：kg）（0，1] （1，2] （2，3] （3，4] （4，5]
包裹件数 43 30 15 8 4
公司对近50天每天承揽包裹的件数（在表2中的“件数范围”内取的一个近似数据）、件数范围及天数，列表如表（表2）：
表2：
件数范围 0～99 100～199 200～299 300～399 400～500
天数 5 10 25 5 5
每天承揽包裹的件数 50 150 250 350 450
（1）将频率视为概率，计算该公司未来3天内恰有1天揽件数在100～299之间的概率；
（2）①根据表1中最近100件包裹的质量统计，估计该公司对承揽的每件包裹收取快递费的平均值：
②根据以上统计数据，公司将快递费的三分之一作为前台工作人员的工资和公司利润，其余用作其他费用．目前，前台有工作人员5人，每人每天揽件数不超过100件，日工资80元．公司正在考虑是否将前台人员裁减1人，试计算裁员前、后公司每天揽件数的数学期望；若你是公司决策者，根据公司每天所获利润的期望值，决定是否裁减前台工作人员1人？

查看解析收藏纠错

+选题
题型：选择题题类：历年真题难易度：易
新测
年份：2019

已知集合A={1，2，3，4}，B={2，4，6}，则集合A∪B中元素的个数为（　　）

A.3 B.4 C.5 D.6

查看解析收藏纠错

+选题
题型：选择题题类：历年真题难易度：较易
新测
年份：2019

若变量x，y满足约束条件则z=x-y的最大值为（　　）

A.8 B.16 C.3 D.4

查看解析收藏纠错

+选题
题型：选择题题类：历年真题难易度：易
新测
年份：2019

已知集合A={x|-1＜x＜3}，B={x|x（x-3）≤0}，则A∪B=（　　）

A.{x|x≤3} B.{x|-1＜x＜3} C.{xl0≤x＜3} D.{x|-1＜x≤3}

查看解析收藏纠错

+选题
题型：选择题题类：历年真题难易度：易
新测
年份：2019

过抛物线y²=4x的焦点F的直线交抛物线于A，B两点，若线段AB的中点M到y轴的距离为2，则|AB|=（　　）

A.8 B.6 C.5 D.4

查看解析收藏纠错

+选题
题型：选择题题类：历年真题难易度：较易
新测
年份：2019

（1+x）（1-2x）⁵的展开式中x³的系数为（　　）

A.-80 B.-40 C.40 D.80

查看解析收藏纠错

+选题

题型：解答题题类：历年真题难易度：较易

新

年份：2019

在考试评价中，客观题难度的计算公式为p_i=

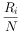，其中p_i只为第i题的难度，R_i为答对该题的人数，N为参加测试的总人数．
现对某校高三年级120名学生进行一次测试，共5道客观题．测试前根据对学生的了解，预估了每道题的难度，如表所示：

题号	1	2	3	4	5
考前预估难度P_i	0.9	0.8	0.7	0.6	0.4

测试后，从中随机抽取了10名学生，将他们编号后统计各题的作答情况，如表所示（“√”表示答对．“×”表示答错）：

题号学生编号	1	2	3	4	5
1	×	√	√	√	√
2	√	√	√	√	×
3	√	√	√	√	×
4	√	√	√	×	×
5	√	√	√	√	√
6	√	×	×	√	×
7	×	√	√	√	×
8	√	×	×	×	×
9	√	√	×	×	×
10	√	√	√	√	×

（1）根据题中数据，将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表：

题号	1	2	3	4	5
实测答对人数
实测难度

并根据上表估计这120名学生中第5题的实测答对人数；
（2）从编号为1到5的5人中随机抽取2人，求恰好有1人答对第5题的概率；
（3）定义统计量S=

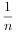[（P₁′-P₁）²+（P₂′-P₂）²+…+（P_n′-P_n）²]，其中P_i′为第i题的实测难度，P_i为第i题的预估难度（i=1，2，..，n）．规定：若S＜0.05，则称该次测试的难度预估合理，否则为不合理．判断本次测试的难度预估是否合理．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心

包裹重量（单位：kg）	（0，1]	（1，2]	（2，3]	（3，4]	（4，5]
包裹件数	43	30	15	8	4

件数范围	0～99	100～199	200～299	300～399	400～500
天数	5	10	25	5	5
每天承揽包裹的件数	50	150	250	350	450