代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：610选择本页全部试题

题型：解答题题类：模拟题难易度：较易
新
年份：2020

如图，在\(\triangle ABC\)中，点\(D\)在边\(BC\)上，\(AC=DC=2\)，\(\sin ∠ABC= \dfrac {4 \sqrt {2}}{9},\cos ∠ADC= \dfrac { \sqrt {3}}{3}\)．
\((1)\)求\(AB\)的长；
\((2)\)求\(\triangle ABC\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

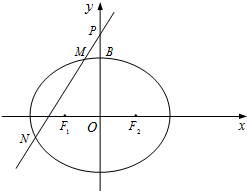已知椭圆\(C\)：\( \dfrac {x^{2}}{a^{2}} + \dfrac {y^{2}}{b^{2}} =1(a > b > 0)\)的左，右焦点分别为\(F _{1}\)，\(F _{2}\)，上顶点为\(B.Q\)为抛物线\(y ^{2} =12x\)的焦点，且\( \overrightarrow {F_{1}B} \boldsymbol{⋅} \overrightarrow {QB} =0\)，\(2 \overrightarrow {F_{1}F_{2}} + \overrightarrow {QF_{1}} =0\)．
\((\)Ⅰ\()\)求椭圆\(C\)的标准方程；
\((\)Ⅱ\()\)过定点\(P(0 , 2)\)的直线\(l\)与椭圆\(C\)交于\(M\)，\(N\)两点\((M\)在\(P\)，\(N\)之间\()\)，设直线\(l\)的斜率为\(k(k > 0)\)，在\(x\)轴上是否存在点\(A(m , 0)\)，使得以\(AM\)，\(AN\)为邻边的平行四边形为菱形？若存在，求出实数\(m\)的取值范围；若不存在，请说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

设函数\(f(x)=\cos x\cdot \sin (x+ \dfrac {π}{3})- \sqrt {3}\cos ^{2}x+ \dfrac { \sqrt {3}}{4}\)，\(x∈R\)．
\((1)\)求\(f(x)\)的最小正周期和对称中心；
\((2)\)若函数\(g(x)=f(x+ \dfrac {π}{4})\)，求函数\(g(x)\)在区间\([- \dfrac {π}{6}, \dfrac {π}{6}]\)上的最值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

\(\triangle ABC\)内角\(A\)，\(B\)，\(C\)所对的边分别为\(a\)，\(b\)，\(c\)，满足\((2b- \sqrt {3}c)\cos A= \sqrt {3}a\cos C\)．
\((1)\)求\(A\)的大小．
\((2)\)如图，若\(AB=4\)，\(AC= \sqrt {3}\)，\(D\)为\(\triangle ABC\)所在平面内一点，\(DB⊥AB\)，\(BC=CD\)，求\(\triangle BCD\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

在\(\triangle ABC\)中，已知\(2S=bc\cos A\)，其中\(S\)为\(\triangle ABC\)的面积，\(a\)，\(b\)，\(c\)分别为角\(A\)，\(B\)，\(C\)的对边．
\((1)\)求角\(A\)的值；
\((2)\)若\(\tan B= \dfrac {6}{5}\)，求\(\sin 2C\)的值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

已知函数\(f(x)=e ^{x} -ae ^{-x} -mx(a , m∈R)\)为奇函数．
\((1)\)讨论\(f(x)\)的单调性；
\((2)\)若\(f(x)\)有极小值\(f(x _{0} )\)，且\(f(x _{0} )\leqslant - \dfrac {2}{e}\)恒成立，求实数\(m\)的最小值．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

在\(\triangle ABC\)中，角\(A\)，\(B\)，\(C\)所对边分别为\(a\)，\(b\)，\(c\)，满足\(2\cos (A-C)=4\sin A\sin C-1\)．
\((\)Ⅰ\()\)若\(b= \sqrt {3}a\)，求角\(A\)；
\((\)Ⅱ\()\)若\(a+c=3\)，\(b= \sqrt {3}\)，求\(\triangle ABC\)的面积\(S\)．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

已知\(S _{n}\)，\(T _{n}\)分别为数列\(\{a _{n} \}\)，\(\{b _{n} \}\)的前\(n\)项和，\(a _{1} =1\)且\(2S _{n} =a _{n+1} -1(n∈N ^{*} ).\)
\((\)Ⅰ\()\)求数列\(\{a _{n} \}\)的通项公式；
\((\)Ⅱ\()\)若对任意正整数\(n\)，都有\(a _{1} b _{n} +a _{2} b _{n-1} +a _{3} b _{n-2} +…+a _{n} b _{1} =3 ^{n} -n-1\)成立，求满足等式\(T _{n} =a _{n}\)的所有正整数\(n\)．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

在平面中，四边形\(ABCD\)满足\(AB⊥AD\)，\(AB=4\)，\(AC=2 \sqrt {5}\)，\(∠BCD=2∠BCA\)，\(\triangle ABC\)的面积为\(4\)．
\((1)\)求\(BC\)的长；
\((2)\)求\(\triangle ACD\)的面积．

查看解析收藏纠错

+选题
题型：解答题题类：模拟题难易度：较易
新
年份：2020

已知数列\(\{a _{n} \}\)的前项和满足\(2S_{n}-na_{n}=n(n∈N^{*})\)，且\(a _{2} =3\)．
\((1)\)求证：数列\(\{ \dfrac {a_{n}-1}{n-1}\}(n\geqslant 2)\)是常数数列；
\((2)\)设\(b_{n}= \dfrac {1}{a_{n} \sqrt {a_{n+1}}+a_{n+1} \sqrt {a_{n}}}\)，\(T _{n}\)为数列\(\{b _{n} \}\)的前\(n\)项和，求使\(T_{n} > \dfrac {9}{20}\)成立的最小正整数\(n\)的值．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心