题型：解答题 题类：模拟题 难易度：较易
新年份：2020
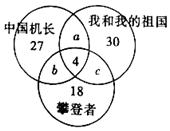在中华人民共和国成立\(70\)周年，国庆期间三大主旋律大片，集体上映，拉开国庆档电影大幕．据统计\(《\)我和我的祖国\(》\)票房收入为\(31.71\)亿元，\(《\)中国机长\(》\)票房收入为\(29.12\)亿元，\(《\)攀登者\(》\)票房收入为\(10.98\)亿元．已知某城市国庆后统计得知大量市民至少观看了一部国庆档大片，在观看的市民中进行随机抽样调查，抽样\(100\)人，其中观看了\(《\)我和我的祖国\(》\)有\(49\)人，\(《\)中国机长\(》\)有\(46\)人，\(《\)攀登者\(》\)有\(34\)人，统计图表如图．题型：解答题 题类：模拟题 难易度：较易
新年份：2020
如图，直四棱柱\(ABCD-A _{1} B _{1} C _{1} D _{1}\)的底面是菱形，\(AA _{1} =4\)，\(AB=2\)，\(∠BAD=60°\)，\(E\)、\(M\)、\(N\)分别是\(BC\)、\(BB _{1}\)、\(A _{1} D\)的中点．
如图，三棱锥\(P-ABC\)中，底面\(\triangle ABC\)是边长为\(2\)的正三角形，\(PA=2\)，\(PA⊥\)底面\(ABC\)，点\(E\)，\(F\)分别为\(AC\)，\(PC\)的中点．
已知函数\(f(x)=A\sin (ωx+φ)(x∈R,A > 0,ω > 0,0 < φ < \dfrac {π}{2})\)的部分图象如图所示．
如图所示，在四棱锥\(P-ABCD\)中，\(PD⊥\)平面\(ABCD\)，\(BD\)是线段\(AC\)的中垂线，\(BD\)与\(AC\)交于点\(O\)，\(AC=8\)，\(PD=2\)，\(OD=3\)，\(OB=5\)．