题型：解答题 题类：历年真题 难易度：较易
新年份：2020
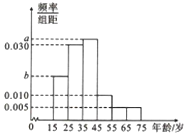2019年全国“两会”，即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国会第二次会议，分别于2019年3月5日和3月3日在北京召开．为了了解哪些人更关注“两会”，某机构随机抽取了年龄在15～75岁之间的200人进行调查，并按年龄绘制出频率分布直方图，如图．| 关注 | 不关注 | 总计 | |
| “青少年” | |||
| “中老年” | |||
| 总计 |
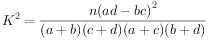，其中n=a+b+c+d．| P（K2≤k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
题型：解答题 题类：历年真题 难易度：较易
新年份：2020
如图所示，用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥，放在水平桌面上，被一阵风吹倒．
已知函数f（x）=Asin（ωx+φ）+b（A＞0，ω＞0，
）的图象如图所示．
个单位长度再把所有点的横坐标变为原来的
（纵坐标不变）得到函数y=g（x）的图象，求出函数y=g（x）的单调递增区间及对称中心． 
，
]上的最小值，并直接写出函数f（x）的一个周期． 
+
=1（a＞b＞0）的离心率为
，A1（-a，0），A2（a，0），B（0，b），△A1BA2的面积为2．
求数列{cn}的前n项和Tn． 
如图所示，为美化环境，拟在四边形ABCD空地上修建两条道路EA和ED，将四边形分成三个区域，种植不同品种的花草，其中点E在边BC的三等分处（靠近B点），BC=3百米，BC⊥CD，∠ABC=120°，
百米，∠AED=60°．
按原来的顺序组成新的数列，试求数列{kn}的通项公式，并求该数列的前n项和Tn． 