代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：5688选择本页全部试题

题型：选择题题类：期末考试难易度：较易
新测
年份：2021

已知三条不重合的直线\(m\)，\(n\)，\(l\)，三个不重合的平面\(α\)，\(β\)，\(γ\)，则\((\quad)\)

A.若\(m⊂α\)，\(n⊂α\)，\(m/\!/β\)，\(n/\!/β\)，则\(α/\!/β\) B.若\(l⊥α\)，\(m⊂β\)，\(l⊥m\)，则\(α/\!/β\) C.若\(α⊥γ\)，\(β⊥γ\)，\(α∩β=l\)，则\(l⊥γ\) D.若\(m/\!/n\)，\(n⊂α\)，则\(m/\!/α\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

已知角\(x\)的终边上一点坐标为\((\sin\dfrac{5π}{6},\cos\dfrac{5π}{6})\)，则角\(x\)的最小正值为\((\quad)\)

A.\(\dfrac{5π}{6}\) B.\(\dfrac{5π}{3}\) C.\(\dfrac{11π}{6}\) D.\(\dfrac{2π}{3}\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

命题“\(∃x_{0}\in R\)，\(x_{0}^{3}-x_{0}^{2}+1>0\)”的否定是\((\quad)\)

A.\(∀x\in R\)，\(x_{}^{3}-x_{}^{2}+1\leqslant 0\) B.\(∃x_{0}\in R\)，\(x_{0}^{3}-x_{0}^{2}+1< 0\) C.\(∃x_{0}\in R\)，\(x_{0}^{3}-x_{0}^{2}+1\leqslant 0\) D.\(∀x\in R\)，\(x_{}^{3}-x_{}^{2}+1>0\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

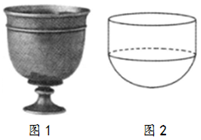唐狩猎纹高足银杯如图\(1\)，\(1963\)年出土于陕西省西安市沙坡村容藏，为唐代的酒具．它的盛酒部分可以近似地看作半球与圆柱的组合体\((\)假设内壁表面光滑，忽略杯壁厚度\()\)，如图\(2\)所示已知半球的半径为\(R\)，酒杯内壁表面积为\(\dfrac{14}{3}πR^{2}\)，设酒杯上部分圆柱的体积为\(V_{1}\)，下部分半球的体积为\(V_{2}\)，则\(\dfrac{V_{1}}{V_{2}}=(\quad)\)

A.\(2\) B.\(\dfrac{3}{2}\) C.\(1\) D.\(\dfrac{3}{4}\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

设锐角三角形\(ABC\)的内角\(A\)，\(B\)，\(C\)所对的边分别为\(a\)，\(b\)，\(c\)，若\(a=2\)，\(B=2A\)，则\(b\)的取值范围为\((\quad)\)

A.\((0,4)\) B.\((2,2\sqrt{3})\) C.\((2\sqrt{2},2\sqrt{3})\) D.\((2\sqrt{2},4)\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

“\(α\)是三角形的内角”是“\(\sin α>0\)”的\((\quad)\)

A.充分但不必要条件 B.必要但不充分条件 C.充要条件 D.既不充分也不必要条件

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

设\(a\in R\)，则“\(a< 1\)”是“\(0< a< 1\)”的\((\quad)\)

A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

\((x-\dfrac{1}{x})^{5}\)展开式中\(x\)的系数为\((\quad)\)

A.\(-20\) B.\(-10\) C.\(10\) D.\(20\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

从\(4\)名高一学生和\(5\)名高二学生中，选\(3\)人参加社区垃圾分类宣传活动，其中至少有\(1\)名高二学生参加宣传活动的不同选法种数为\((\quad)\)

A.\(50\) B.\(70\) C.\(80\) D.\(140\)

查看解析收藏纠错

+选题
题型：选择题题类：期末考试难易度：较易
新测
年份：2021

已知\(f(x)=x^{2}-2kx+3k^{2}-3k+1(k\in R).\)以下四个命题：
①对任意实数\(x\)，存在\(k\)，使得\(f(x)>0\)；
②对任意\(k\)，存在实数\(x\)，使得\(f(x)>0\)；
③对任意实数\(k\)，\(x\)，均有\(f(x)>0\)成立；
④对任意实数\(k\)，\(x\)，均有\(f(x)< 0\)成立．
其中所有正确的命题是\((\quad)\)

A.①② B.②③ C.①③ D.②④

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心