题型：填空题 题类：其他 难易度：较难
年份：2018
\((1)\)设抛物线\({x}^{2}=4y \)上一点\(P\)到其焦点\(F\)的距离为\(3\)，则点\(P\)的纵坐标为_________．
\((2)\)已知函数\(f\left(x\right)=kx-\ln x \)在\(x=1 \)处的导数值为\(0\)，则实数\(k\)的值为_________．
\((3)\)某校高三年级共有\(800\)名学生，现采用系统抽样的方法，抽取\(25\)名学生做问卷调查，将这\(800\)名学生按\(1\)，\(2\)，\(...\)，\(800\)随机编号，按编号顺序平均分组\(.\)若从第\(5\)组抽取的编号为\(136\)，则从第\(2\)组中抽取的编号为_________．
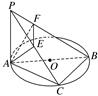
\((4)\)如图\(PA⊥⊙O\)所在平面，\(AB\)是\(⊙O\)的直径，\(C\)是\(⊙O\)上一点，\(AE⊥PC\)，\(AF⊥PB\)，给出下列结论：\(①AE⊥BC\)；\(②EF⊥PB\)；\(③AF⊥BC\)；\(④AE⊥\)平面\(PBC\)，其中真命题的序号是______．
题型：选择题 题类：其他 难易度：较难
测年份：2018
题型：选择题 题类：其他 难易度：较难
测年份：2018
设\(m,n\)是两条不同的直线，\(\alpha ,\beta \)是两个不同的平面，下列命题中正确的个数是\((\) \()\)
\(①\)若\(m/\!/\alpha \)，\(m/\!/\beta \)，则\(\alpha /\!/\beta \) \(②\)若\(\alpha /\!/\beta \)，\(m\subset \alpha \)，\(n\subset \beta \)，则\(m/\!/n\)
\(③\)若\(\alpha /\!/\beta \)，\(m/\!/n\)，\(m/\!/\alpha \)，则\(n/\!/\beta \) \(④\)若\(m/\!/\alpha \)，\(m\subset \beta \)，\(α∩β=n \)，则\(m/\!/n\)
\(⑤m⊂α,n∩α=A,点A∉m, \)则\(n\)与\(m\)不共面；
题型：选择题 题类：其他 难易度：较难
测年份：2018
设\(m\)、\(n\)是两条不同的直线，\(α\)、\(β\)是两个不同的平面，考查下列结论，其中正确的是( )
已知：a∥α，a∥β，α∩β=b（如图所示），求证：a∥b． 
