题型：填空题 题类：期末考试 难易度：中档
年份：2018
\(13.(1)\)如果\(\cos \alpha =\dfrac{1}{3}\)，且\(\alpha \)是第四象限的角，那么\(\cos \left(α+ \dfrac{π}{2}\right)= \)_____________。
\((2)\)设变量\(x,y\)满足约束条件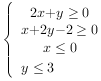
，则目标函数\(z=x+y\)的最大值为_______________。
\((3)\)已知向量\(\overrightarrow{a}=(-1,2),\ \ \overrightarrow{b}=(m,1)\)，若向量\(\overrightarrow{a}+2\overrightarrow{b}\)与\(\overrightarrow{a}\)平行，则\(m=\)_____．
\((4)\)若\(\lg m+\lg n=2,\) 则\(\dfrac{1}{m}+\dfrac{2}{n}\)的最小值是______
题型：填空题 题类：期末考试 难易度：中档
年份：2018
\((1)\)在等比数列\(\{a_{n}\}\)中，公比\(q=2\)，前\(n\)项和为\(S_{n}\)，若\(S_{5}=1\)，则\(S_{10}=\)________．
\((2)\)若实数\(x\)，\(y\)满足约束条件\(\begin{cases}\begin{matrix}2x-y-2\leqslant 0 \\ 2x+y-4\geqslant 0\end{matrix} \\ y\leqslant 2\end{cases} \)则\(\dfrac{y}{x}\)的取值范围是________．
\((3)\)已知点\((1,2)\)与\((-1,m)\)关于直线\(kx-y+3=0\)对称，则\(m+k=\)________．
\((4)\)已知\(\triangle ABC\)的内角\(A\)，\(B\)，\(C\)所对的边分别为\(a\)，\(b\)，\(c\)，且\(\dfrac{\sin A\cos B}{\sin B}=\sqrt{3}-\cos A\)，则\(\dfrac{c}{b}=\)________．
题型：填空题 题类：期末考试 难易度：中档
年份：2018
\((1)\)直线\(y=x+2\)与圆\({{x}^{2}}+{{y}^{2}}-4x-12=0\)交于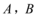
两点，则\(\left| AB \right|=\)________．
\((2)\)在某次数学考试中，甲、乙、丙三名同学中只有一个人得了优秀\(.\)当他们被问到谁得到了优秀时，丙说：“甲没有得优秀”；乙说：“我得了优秀”；甲说：“丙说的是真话”，事实证明：在这三名同学中，只有一人说的是假话，那么得优秀的同学是____．
\((3)\)已知三棱锥\(P-ABC\)，\(PA⊥\)面\(ABC\)，\(AB⊥BC\)，且\(PA=AB=BC=2\)，则三棱锥\(P-ABC\)的外接球的表面积为______．
\((4)\)某高中准备租用甲、乙两种型号的客车安排\(900\)名学生去外地研究性学习\(.\)甲、乙两种车辆的载客量分别为\(36\)人\(/\)辆和\(60\)人\(/\)辆，租金分别为\(400\)元\(/\)辆和\(600\)元\(/\)辆，学校要求租车总数不超过\(21\)辆，且乙型车不多于甲型车\(7\)辆，则学校所花租金最少为____元．
，满足f（x）＝3的x的值是________．
的最大值为________，最小值为________．