题型:填空题 题类:模拟题 难易度:较难
年份:2018
\((1)\)设\(\alpha \)为锐角, 若\(\cos \left( \alpha +\dfrac{\pi }{6} \right)=\dfrac{4}{5}\),则\(\sin \alpha \)的值为_________.
\((2)\)在边长为\(2\)的正三角形\(ABC\)中,设\(\overrightarrow{BC}=2 \overrightarrow{BD}, \overrightarrow{CA}=3 \overrightarrow{CE} \),则\(\overrightarrow{AD}\cdot \overrightarrow{BE}=\)_____________.
\((3)\)已知正四面体\(ABCD\)中,\(E\)是\(AB\)的中点,则异面直线\(CE\)与\(BD\)所成角的余弦值为__________.
\((4)\)若\(f\left( x \right)=A{\sin }\left( \omega +\varphi \right)+3(\omega > 0,\left| \varphi \right| < { }\!\!\pi\!\!{ })\)对任意实数\(t\)都有\(f\left( t+\dfrac{{ }\!\!\pi\!\!{ }}{3} \right)=f\left( -t+\dfrac{{ }\!\!\pi\!\!{ }}{3} \right).\)记\(g\left( x \right)=A{\cos }\left( \omega x+\varphi \right)-2\),则\(g\left( \dfrac{{ }\!\!\pi\!\!{ }}{3} \right)=\)_______.
题型:解答题 题类:模拟题 难易度:较难
年份:2018
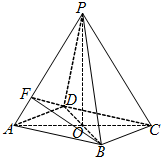 如图所示,在四棱锥\(P-ABCD\)中,底面四边形\(ABCD\)是菱形,\(AC∩BD=O\),\(\triangle PAC\)是边长为\(2\)的等边三角形,\(PB=PD= \sqrt {6}\),\(AP=4AF\).
如图所示,在四棱锥\(P-ABCD\)中,底面四边形\(ABCD\)是菱形,\(AC∩BD=O\),\(\triangle PAC\)是边长为\(2\)的等边三角形,\(PB=PD= \sqrt {6}\),\(AP=4AF\).