题型:解答题 题类:月考试卷 难易度:较难
年份:2018
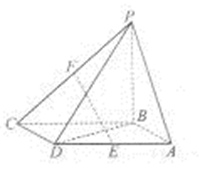
\((1)\)求证:平面\(PAD\bot \)平面\(ABCD\);
\((2)\)若直线\(PC\)与\(AB\)所成角的正切值为\(\dfrac{1}{2}\),求直线\(BM\)与平面\(PDB\)所成角的正弦值.
题型:解答题 题类:月考试卷 难易度:较难
年份:2018
\((1)\)抛物线\(y=x^{2}\)在\(x=2\)处的切线与抛物线以及\(x\)轴所围成的曲边图形的面积为________.
\((2)\)设\(\triangle ABC\)中,角\(A\),\(B\),\(C\)所对的边分别为\(a\),\(b\),\(c\),若\(a=2\),\(c=2\sqrt{3}\),\(\cos A=\dfrac{\sqrt{3}}{2}\),则\(b=\)________.
\((3)\)在三棱锥\(A—BCD\)中,底面\(BCD\)为边长为\(2\)的正三角形,顶点\(A\)在底面\(BCD\)上的射影为\(\triangle BCD\)的中心,若\(E\)为\(BC\)的中点,且直线\(AE\)与底面\(BCD\)所成角的正切值为\(2\sqrt{2}\),则三棱锥\(A—BCD\)外接球的表面积为________.
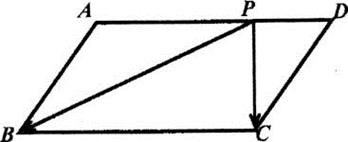
\((4)\)在面积为\(2\)的平行四边形\(ABCD\)中,点\(P\)为直线\(AD\)上的动点,则\(\overrightarrow{PB}\cdot \overrightarrow{PC}+{{\overrightarrow{BC}}^{2}}\)的最小值是________.
题型:解答题 题类:月考试卷 难易度:较难
年份:2018
如图,\(P\)是菱形\(ABCD\)所在平面外一点,\(\angle BAD={{60}^{{}^\circ }}\),\(\Delta PCD\)是等边三角形,\(AB=2\),\(PA=2\sqrt{2}\),\(M \)是\(PC\)的中点,点\(G\)为线段\(DM\)上一点\((\)端点除外\()\),平面\(APG\)与\(BD\)交于点\(H\).
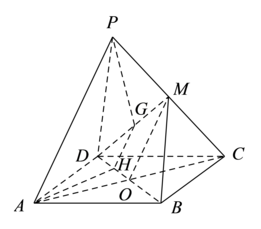
\((1)\)求证:\(PA/\!/GH\);
\((2)\)求证:\(BD\bot \)平面\(PAC\);
\((3)\)求\(AC\)与平面\(BDM\)所成角的正弦值.
题型:选择题 题类:月考试卷 难易度:较难
测年份:2018
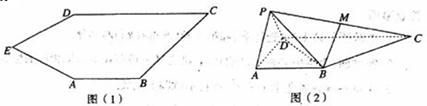
如图,已知四边形\(ABCD\)是正方形,\(∆ABP \),\(∆BCQ \),\(∆CDR \),\(∆DAS \)都是等边三角形,\(E\)、\(F\)、\(G\)、\(H\)分别是线段\(AP\)、\(DS\)、\(CQ\)、\(BQ\)的中点,分别以\(AB\)、\(BC\)、\(CD\)、\(DA\)为折痕将四个等边三角形折起,使得\(P\)、\(Q\)、\(R\)、\(S\)四点重合于一点\(P\),得到一个四棱锥\(.\)对于下面四个结论:
\(①EF\)与\(GH\)为异面直线;\(②\)直线\(EF\)与直线\(PB\)所成的角为\(60^{\circ} \)
\(③EF/\!/ \)平面\(PBC\); \(④\)平面\(EFGH/\!/ \)平面\(ABCD\);
其中正确结论的个数有\((\) \()\)
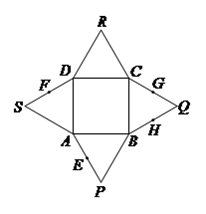
题型:解答题 题类:月考试卷 难易度:较难
年份:2018
如图,四棱锥\(P-ABCD\)的底面\(ABCD\)是平行四边形,\(BA=BD= \sqrt{2} \),\(AD=2\),\(PA=PD=\sqrt{5} \),\(E\),\(F\)分别是棱\(AD\),\(PC\)的中点.