代数-数学-知识点同步搜题

选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2025 2024 2023 2022 2021 2020 更早

总题量：5046选择本页全部试题

题型：解答题题类：其他难易度：难
新
年份：2020

已知数列\(\{a _{n} \}\)中的相邻两项\(a _{2k-1}\)、\(a _{2k}\)是关于\(x\)的方程\(x ^{2} -(3k+2 ^{k} )x+3k\boldsymbol{⋅}2 ^{k} =0\)的两个根，且\(a _{2k-1} \leqslant a _{2k} (k=1 , 2 , 3 , …)\)．
\((\)Ⅰ\()\)求\(a _{1}\)，\(a _{3}\)，\(a _{5}\)，\(a _{7}\)及\(a _{2n} (n\geqslant 4)(\)不必证明\()\)；
\((\)Ⅱ\()\)求数列\(\{a _{n} \}\)的前\(2n\)项和\(S _{2n}\)．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

如图，已知\(ABCD-A _{1} B _{1} C _{1} D _{1}\)是棱长为\(a\)的正方体，\(E\)、\(F\)分别为棱\(AA _{1}\)与\(CC _{1}\)的中点，求四棱锥的\(A _{1} -EBFD _{1}\)的体积．

查看解析收藏纠错

+选题
题型：选择题题类：其他难易度：难
新测
年份：2020

已知\(\sin 10°=k\)，则\(\cos 620°\)等于\((\:\:\:\:)\)

A.\(k\) B.\(-k\) C.\(±k\) D.\( \sqrt {1-k^{2}}\)

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

是否存在实数\(p\)，使\(4x+p < 0\)是\(x ^{2} -x-2 > 0\)的充分条件？如果存在，求出\(p\)的取值范围；否则，说明理由．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

设函数\(f(x)\)在\(R\)上是偶函数，在区间\((-∞ , 0)\)上递增，且\(f(2a ^{2} +a+1) < f(2a ^{2} -2a+3)\)，求\(a\)的取值范围．

查看解析收藏纠错

+选题
题型：选择题题类：其他难易度：难
新测
年份：2020

定义：设\(M\)是非空实数集，若\(∃a∈M\)，使得对于\(∀x∈M\)，都有\(x\leqslant a(x\geqslant a)\)，则称\(a\)是\(M\)的最大\((\)小\()\)值．若\(A\)是一个不含零的非空实数集，且\(a _{0}\)是\(A\)的最大值，则\((\:\:\:\:)\)

A.当\(a _{0} > 0\)时，\(a _{0} ^{-1}\)是集合\(\{x ^{-1} |x∈A\}\)的最小值 B.当\(a _{0} > 0\)时，\(a _{0} ^{-1}\)是集合\(\{x ^{-1} |x∈A\}\)的最大值 C.当\(a _{0} < 0\)时，\(-a _{0} ^{-1}\)是集合\(\{-x ^{-1} |x∈A\}\)的最小值 D.当\(a _{0} < 0\)时，\(-a _{0} ^{-1}\)是集合\(\{-x ^{-1} |x∈A\}\)的最大值

查看解析收藏纠错

+选题
题型：填空题题类：其他难易度：难
新
年份：2020

到\(A(2 , -3)\)和\(B(4 , -1)\)的距离相等的点的轨迹方程是______．

查看解析收藏纠错

+选题
题型：填空题题类：其他难易度：难
新
年份：2020

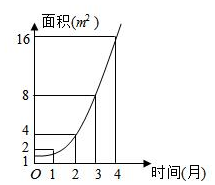
如图是某池塘中野生水葫芦的面积与时间的函数关系图象．假设其函数关系为指数函数，并给出下列说法：

①此指数函数的底数为\(2\)；
②在第\(5\)个月时，野生水葫芦的面积会超过\(30m ^{2}\)；
③野生水葫芦从\(4m ^{2}\)蔓延到\(12m ^{2}\)只需\(1.5\)个月；
④设野生水葫芦蔓延至\(2m ^{2}\)、\(3m ^{2}\)、\(6m ^{2}\)所需的时间分别为\(t _{1}\)、\(t _{2}\)、\(t _{3}\)则有\(t _{1} +t _{2} =t _{3}\)；
其中正确的说法有________\(.(\)请把正确的说法的序号都填在横线上\()\)．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

设函数\(f(x)= \dfrac {1-a^{x}}{1+a^{x}} (a > 0\)且\(a\neq 1)\)．
\((\)Ⅰ\()\)求函数\(f(x)\)的定义域，并判断它的奇偶性；
\((\)Ⅱ\()\)若\(f(x)\geqslant \dfrac {1}{2}\)，求\(x\)的取值范围．

查看解析收藏纠错

+选题
题型：解答题题类：其他难易度：难
新
年份：2020

已知数列\(\{a _{n} \}\)的首项\(a_{1}= \dfrac {2}{3}\)，\(a_{n+1}= \dfrac {2a_{n}}{a_{n}+1},n=1,2,3…\)．
\((1)\)证明：数列\(\{ \dfrac {1}{a_{n}}-1\}\)是等比数列；
\((2)\)求数列\(\{ \dfrac {n}{a_{n}}\}\)的前\(n\)项和为\(S _{n}\)．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心