选择知识点

题型：

全部选择题填空题解答题

难易程度：

全部易较易中档较难难

题类筛选：

全部历年真题模拟题期末考试期中考试月考试卷单元测试其他

年份：

全部 2022 2021 2020 2019 2018 2017 更早

总题量：368选择本页全部试题

题型：解答题题类：历年真题难易度：较易
新
年份：2019

在△ABC中，内角A、B、C的对边分别为a、b、c，且满足sin²A＋sin Asin B－6sin²B＝0.

(1)求的值；

(2)若，求sin B的值.

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易
新
年份：2019

在△ABC中，角A，B，C的对边分别为a，b，c，a=3，，．
（Ⅰ）求c的值；
（Ⅱ）若D为BC边上的点，并且，求∠ADB．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易
新
年份：2019

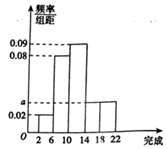某工厂共有200名工人，已知这200名工人去年完成的产品数都在区间[2，22]（单位：万件）内，其中每年完成14万件及以上的工人为优秀员工，现将其分成5组，第1组、第2组、第3组、第4组、第5组对应的区间分别为[2，6），[6，10），[10，14），[14，18），[18，22]，并绘制出如图所示的频率分布直方图．
（1）求a的值，并求去年优秀员工人数；
（2）选取合适的抽样方法从这200名工人中抽取容量为25的样本，求这5组分别应抽取的人数；
（3）现从（2）中25人的样本中的优秀员工中随机选取2名传授经验，求选取的2名工人在同一组的概率．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易
新
年份：2019

三角形ABC中，角A、B、C所对边分别为a，b，c，且sinB=．
（1）若cosA=，求sinC的值；
（2）若b=，sinA=3sinC，求三角形ABC的面积．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易
新
年份：2019

已知整数n，k满足n＞k≥3，集合M={1，2，3，…，n}的所有子集中，含有k个元素的子集记为，这些子集的所有元素之和记为T（n，k），记m_i为A_i中的最小元素，
（1）求T（6，4）与P（6，4）；
（2）化简：、

查看解析收藏纠错

+选题

题型：解答题题类：历年真题难易度：较易

新

年份：2019

随着电子阅读的普及，传统纸质媒体遭受到了强烈的冲击．某杂志社近9年来的纸质广告收入如表所示：

年份	2010	2011	2012	2013	2014	2015	2016	2017	2018
时间代号t	1	2	3	4	5	6	7	8	9
广告收入y（千万元）	2	2.2	2.5	2.8	3	2.5	2.3	2	1.8

根据这9年的数据，对t和y作线性相关性检验，求得样本相关系数的绝对值为0.243；根据后5年的数据，对t和y作线性相关性检验，求得样本相关系数的绝对值为0.984．
（Ⅰ）如果要用线性回归方程预测该杂志社2019年的纸质广告收入，现在有两个方案，
方案一：选取这9年数据进行预测；方案二：选取后5年数据进行预测．
从实际生活背景以及线性相关性检验的角度分析，你觉得哪个方案更合适？
附：
相关性检验的临界值表：

n-2	小概率
n-2	0.05	0.01
3	0.878	0.959
7	0.666	0.798

（Ⅱ）某购物网站同时销售某本畅销书籍的纸质版本和电子书，据统计，在该网站购买该书籍的大量读者中，只购买电子书的读者比例为50%，纸质版本和电子书同时购买的读者比例为10%现用此统计结果作为概率若从上述读者中随机调查了3位，求购买电子书人数多于只购买纸质版本人数的概率．

查看解析收藏纠错

+选题

题型：解答题题类：历年真题难易度：较易
新
年份：2019

某市为了解社区群众体育活动的开展情况，拟采用分层抽样的方法从A，B，C三个行政区中抽出6个社区进行调查．已知A，B，C行政区中分别有12，18，6个社区．
（Ⅰ）求从A，B，C三个行政区中分别抽取的社区个数；
（Ⅱ）若从抽得的6个社区中随机的抽取2个进行调查结果的对比，求抽取的2个社区中至少有一个来自A行政区的概率．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易
新
年份：2019

为了进一步推动全市学习型党组织、学习型社会建设，某市组织开展“学习强国”知识测试，每人测试文化、经济两个项目，每个项目满分均为60分．从全体测试人员中随机抽取了100人，分别统计他们文化、经济两个项目的测试成绩，得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下：
经济项目测试成绩频率分布直方图

分数区间频数

[0，10） 2

[10，20） 3

[20，30） 5

[30，40） 15

[40，50） 40

[50，60] 35

文化项目测试成绩频数分布表
将测试人员的成绩划分为三个等级如下：分数在区间[0，30）内为一般，分数在区间[30，50）内为良好，分数在区间[50，60]内为优秀．
（1）在抽取的100人中，经济项目等级为优秀的测试人员中女生有14人，经济项目等级为一般或良好的测试人员中女生有34人．填写下面列联表，并根据列联表判断是否有95%以上的把握认为“经济项目等级为优秀”与性别有关？

优秀一般或良好合计

男生数

女生数

合计

（2）用这100人的样本估计总体．
（i）求该市文化项目测试成绩中位数的估计值．
（ii）对该市文化项目、经济项目的学习成绩进行评价．
附：

P（K²≥k） 0.150 0.050 0.010

k 2.072 3.841 6.635

．

查看解析收藏纠错

+选题
题型：解答题题类：历年真题难易度：较易
新
年份：2019

在由教育部主办的“高雅艺术进校园”活动中，某知名大学“空谷合唱团”于2018年10月28日晚在某市体育馆举行了大型公益专场音乐会，对弘扬民族文化、提高艺术素养起到了引领作用．活动结束后，随机抽取了300名观众进行调查评分，其频率分布直方图如图：
（1）求a的值和这300名观众评分的中位数；
（2）以样本的频率作概率，评分在“88分及以上”确定为“音乐迷”，现从所有观众中随机地抽取3人作进一步的访谈，用ξ表示抽出3人中“音乐迷”的人数，求ξ的分布列及数学期望．

查看解析收藏纠错

+选题

题型：解答题题类：历年真题难易度：较易

新

年份：2019

在考试评价中，客观题难度的计算公式为p_i=

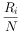，其中p_i只为第i题的难度，R_i为答对该题的人数，N为参加测试的总人数．
现对某校高三年级120名学生进行一次测试，共5道客观题．测试前根据对学生的了解，预估了每道题的难度，如表所示：

题号	1	2	3	4	5
考前预估难度P_i	0.9	0.8	0.7	0.6	0.4

测试后，从中随机抽取了10名学生，将他们编号后统计各题的作答情况，如表所示（“√”表示答对．“×”表示答错）：

题号学生编号	1	2	3	4	5
1	×	√	√	√	√
2	√	√	√	√	×
3	√	√	√	√	×
4	√	√	√	×	×
5	√	√	√	√	√
6	√	×	×	√	×
7	×	√	√	√	×
8	√	×	×	×	×
9	√	√	×	×	×
10	√	√	√	√	×

（1）根据题中数据，将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表：

题号	1	2	3	4	5
实测答对人数
实测难度

并根据上表估计这120名学生中第5题的实测答对人数；
（2）从编号为1到5的5人中随机抽取2人，求恰好有1人答对第5题的概率；
（3）定义统计量S=

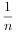[（P₁′-P₁）²+（P₂′-P₂）²+…+（P_n′-P_n）²]，其中P_i′为第i题的实测难度，P_i为第i题的预估难度（i=1，2，..，n）．规定：若S＜0.05，则称该次测试的难度预估合理，否则为不合理．判断本次测试的难度预估是否合理．

查看解析收藏纠错

+选题

高中

选择知识点

服务介绍

帮助中心

分数区间	频数
[0，10）	2
[10，20）	3
[20，30）	5
[30，40）	15
[40，50）	40
[50，60]	35

	优秀	一般或良好	合计
男生数
女生数
合计

P（K²≥k）	0.150	0.050	0.010
k	2.072	3.841	6.635